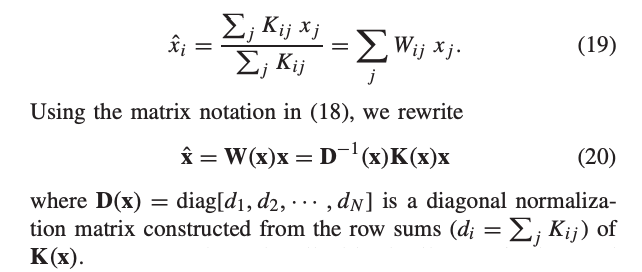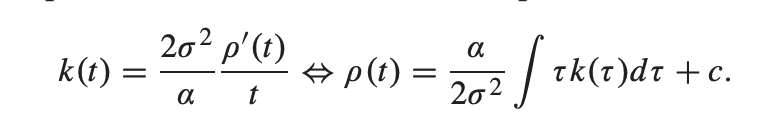Optimization problems for solving inverse problems often require compute-heavy, large-scale, iterative solutions.
Maybe we can avoid all that & "kernelize" the problem, thereby approximating the solution by making & applying a 1-shot filter?
Thread https://ieeexplore.ieee.org/document/8611353
Maybe we can avoid all that & "kernelize" the problem, thereby approximating the solution by making & applying a 1-shot filter?
Thread https://ieeexplore.ieee.org/document/8611353
Variational losses include regularization terms that enable control of desired properties of the solutions. Examples include maximum a-posteriori (MAP) or minimum mean-squared error (MMSE) estimation. But their solutions can be computationally intractable. Consider denoising
2/n
2/n
Depending on the properties of φ the solution may be hard to find explicitly, or even iteratively. But sometimes we can instead derive a kernel K(i,j) from φ, and approximate the solution as a (pseudo-) linear filter. That is, a data-dependent weighted sum like x̂ = W(x)*x
3/n
3/n
This would be really convenient, but what does the kernel K(i,j), or the weights W(i,j), need to be in order to give an approximate solution to the optimization problem in one shot?
The punchline: We must have the Laplacian of W(x) be proportional to the Gradient of φ(x) !
4/n
The punchline: We must have the Laplacian of W(x) be proportional to the Gradient of φ(x) !
4/n
Now specialize to φ(x) = ρ( ||Ax|| ) where A= R(|i-j|) makes a stationary & isotropic kernel that depends only on the (not necessarily local) distance between patches centered at i and j. More generally, this is summed over some or all the locations across the image.
5/n
5/n
Stationary & isotropic kernels are essentially defined in 1D. So using the scalar t = ||A x|| makes it easy to state the relationship between the isotropic kernel k(t) and it's corresponding ρ(t) as follows:
(α and c are constants that must be set accordingly in each case)
6/n
(α and c are constants that must be set accordingly in each case)
6/n
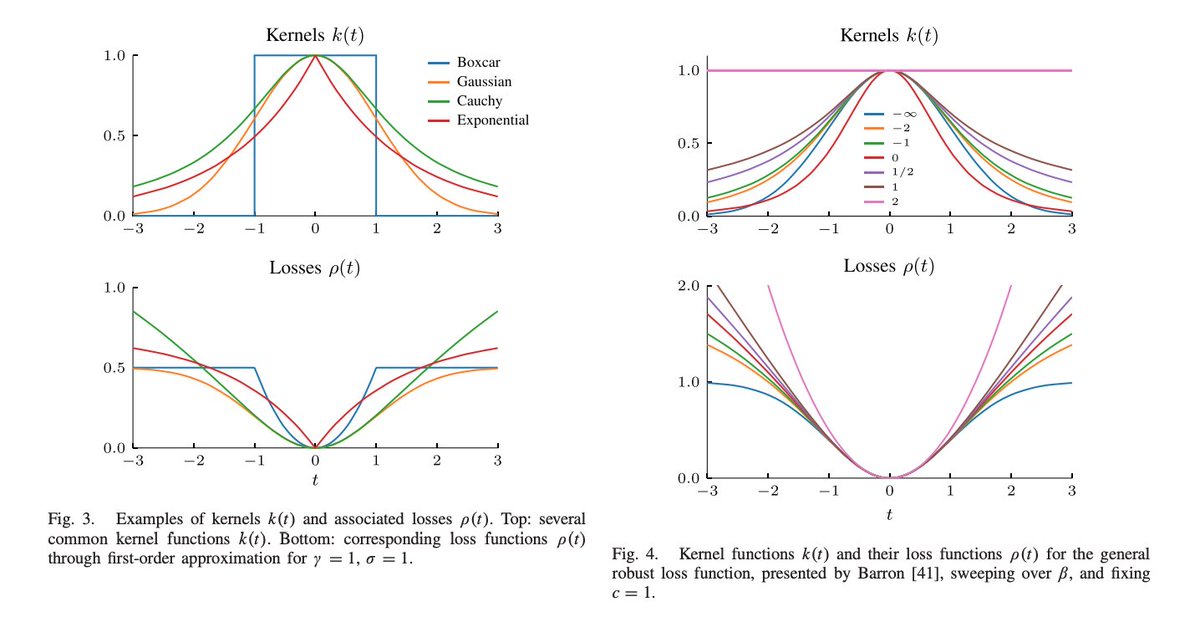
Skipping (lots) of fun details, here are some familiar examples, with nice intuition arising from each case.
7/n
7/n
And here are more examples in graphical form.
You can go in both directions in fact:
L: Set kernel --> get the loss (this give you a Bayesian interpretation of a kernel filter)
R: Set loss --> get the kernel (this gives the empirical Bayes approximation using the kernel)
8/n
You can go in both directions in fact:
L: Set kernel --> get the loss (this give you a Bayesian interpretation of a kernel filter)
R: Set loss --> get the kernel (this gives the empirical Bayes approximation using the kernel)
8/n
Summary
A regularized inverse problem that's hard to solve directly may be approximated by just building & applying a (pseudo-linear) kernel filter directly
Conversely: Given a kernel filter, you could interpret this as an empirical Bayes solution
Fin https://ieeexplore.ieee.org/document/8611353
A regularized inverse problem that's hard to solve directly may be approximated by just building & applying a (pseudo-linear) kernel filter directly
Conversely: Given a kernel filter, you could interpret this as an empirical Bayes solution
Fin https://ieeexplore.ieee.org/document/8611353

 Read on Twitter
Read on Twitter