Read on Twitter
Excited to present my first preprint 
- "Keep the Gradients Flowing: Using Gradient Flow to Study Sparse Network Optimization" , with @sarahookr and @BenjaminRosman .
https://arxiv.org/abs/2102.01670 .
We use Gradient Flow (GF) to study sparse network optimization.
- "Keep the Gradients Flowing: Using Gradient Flow to Study Sparse Network Optimization" , with @sarahookr and @BenjaminRosman . https://arxiv.org/abs/2102.01670 .We use Gradient Flow (GF) to study sparse network optimization.
That is to say, we use GF to study how sparse networks are affected by different optimizers, activation functions, architectures, learning rates and regularizers.
This follows on promising GF work - https://arxiv.org/abs/2010.03533 (by @utkuevci) and https://arxiv.org/abs/2002.07376 .
This follows on promising GF work - https://arxiv.org/abs/2010.03533 (by @utkuevci) and https://arxiv.org/abs/2002.07376 .
1. Firstly, to study sparse networks, we propose a simple, empirical framework - Same Capacity Sparse vs Dense Comparison (SC-SDC). The key idea is to compare sparse networks to their equivalent dense counterparts (same number of connections and same initial weight init).
2. Secondly, we also propose a new, normalized, layerwise measure of gradient flow, Effective Gradient Flow (EGF). EGF is normalized by the number of active weights and distributed evenly across all the layers. We show EGF correlates better, than other GF measures, to ...
performance in sparse networks and hence it is a good formulation for studying the training dynamics of sparse networks.
3.1 Using EGF and SC-SDC, we show that BatchNorm is more important for sparse networks than it is for dense networks (the result is statistically significant), which suggests that gradient instability is a key obstacle to starting sparse.
3.2 We show that optimizers that use an exponentially weighted moving average (EWMA) to obtain an estimate of the variance of the gradient, such as Adam and RMSProp, are sensitive to higher gradient flow. This could explain why these methods are more sensitive to L2 and data aug.
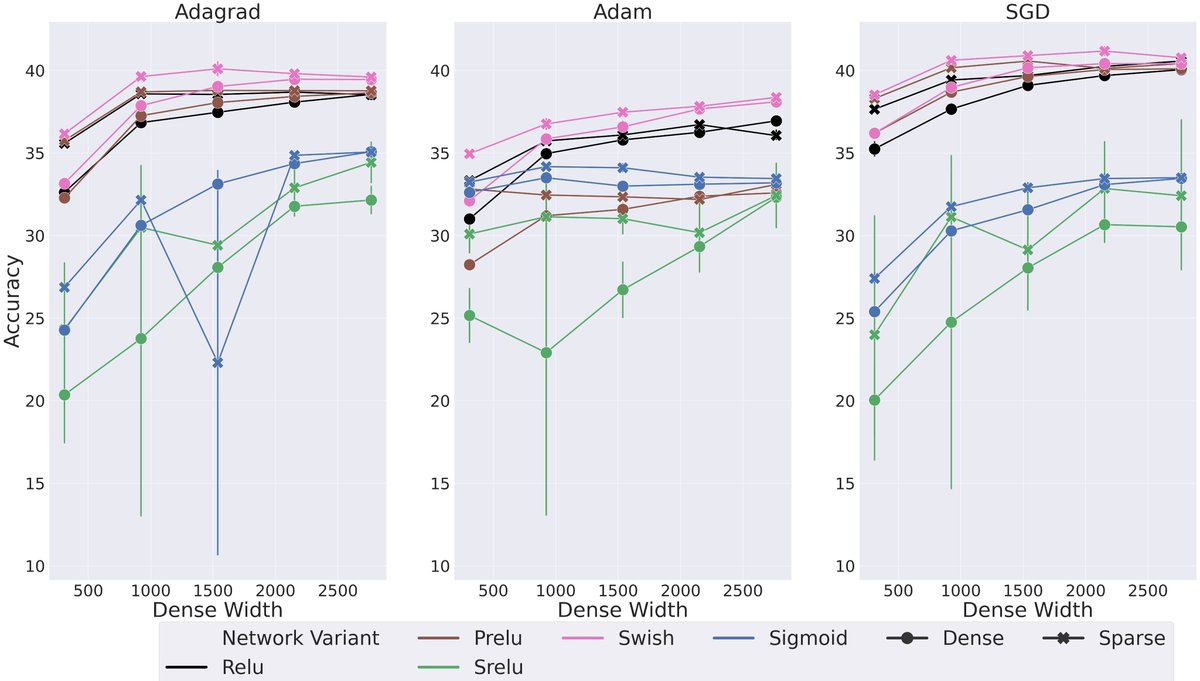
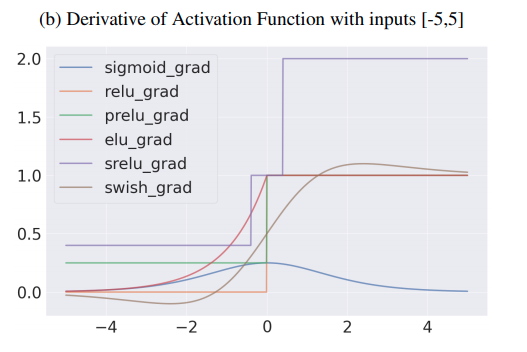
3.3 Finally, we show that Swish and PReLU (when using SGD) are promising activation functions, especially for sparse networks. For the Swish result, we suggest this could be due to Swish’s non-monotonic formulation, that allows for negative gradient flow, which helps with 3.2.
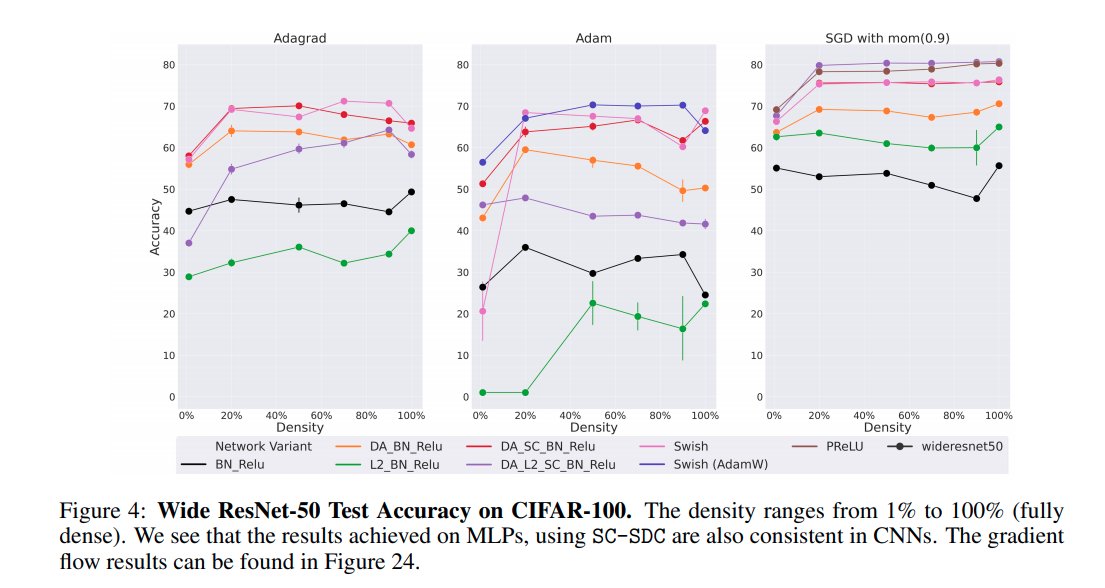
We also extend some of these results from MLPs -> CNNs and from random, fixed sparse networks -> magnitude pruned networks.
In conclusion, our work agrees with and contributes to the literature that emphasizes that initialization is only one piece of the puzzle and taking a wider view of tailoring optimization to sparse networks yields promising results.
Thanks for reading. Also, please let us know if we missed any related work/results and if you have any feedback 
:)
:)
