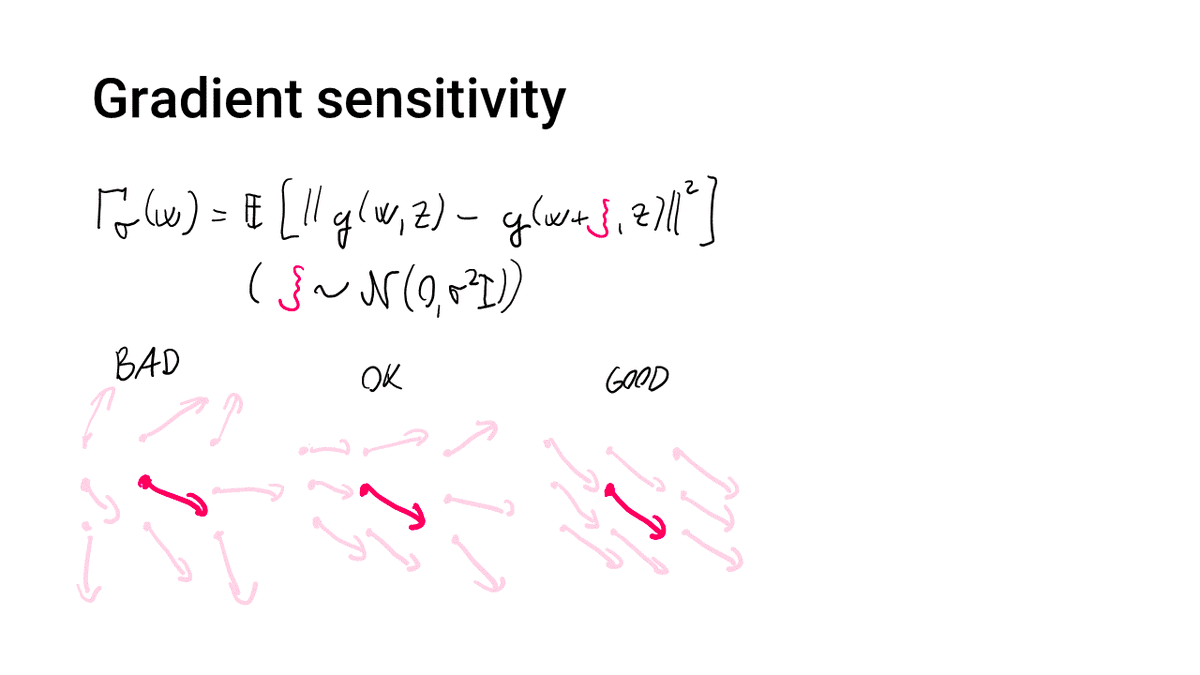MYSTERY: why does SGD generalize well? My new paper may provide some answers: a perturbation analysis identifies three factors that contribute to good generalization. "Flatness" is one of them.
(And yes, the analysis is information-theoretic.)
https://arxiv.org/abs/2102.00931
1/
(And yes, the analysis is information-theoretic.)
https://arxiv.org/abs/2102.00931
1/
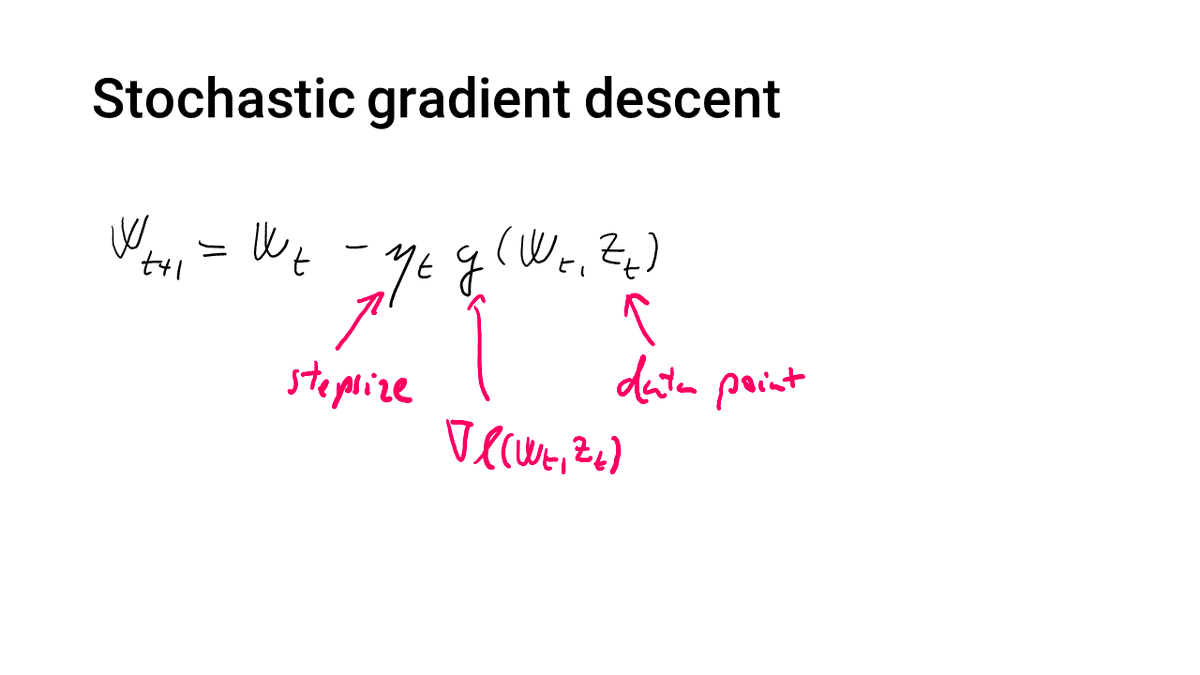
SGD: the algorithm that we all know and love. We consider it for minimizing a general (non-convex) differentiable loss, by doing multiple passes over the data set S = (Z_1,...,Z_n). The stepsize schedule and sampling rule are fixed but arbitrary.
2/
2/
The main result is a generalization-error bound that depends on 3 key quantities:
- The variance of the gradients along the SGD path,
- the perturbation-sensitivity of the gradients along the SGD path, and
- the perturbation-sensitivity of the loss at the final output.
3/
- The variance of the gradients along the SGD path,
- the perturbation-sensitivity of the gradients along the SGD path, and
- the perturbation-sensitivity of the loss at the final output.
3/
The bound involves some tradeoff parameters σ that are independent of the algorithm. This means that the bound holds true for every possible choice of σ, and in particular the one that minimizes the bound---no need for hyperparameter-tuning!
4/
4/
The gradient variance V measures the variability of the gradients with respect to the randomness of the data. This term is small if the gradients are consistent between data points, as measured by the L2 norm.
5/
5/
The gradient sensitivity Γ measures the variability of the gradients with respect to small changes to the parameter vector. This term is small if the gradients are "spatially consistent", as measured by the L2 norm---essentially a local measure of smoothness.
6/
6/
The value sensitivity Δ measures the variability of the loss function to small changes to the parameter vector. This term is small if the training and test loss functions are flat around the final solution produced by SGD.
7/
7/
These three quantities depend on the parametrization and are sometimes at conflict: one cannot be made arbitrarily small without making another one huge. This fig sketches some possible tradeoffs for 3 parametrizations.
8/
8/
Is it possible then to measure V, Γ and Δ under the most favorable parametrization? Turns out that this is indeed possible: our bound holds simultaneously for *all* parametrizations!
9/
9/
The quantities appearing in the bound are defined in terms of perturbations of general covariance matrices, which allows measuring the gradients and the flatness of the objective in various geometries.
10/
10/
One way to read this result is that "SGD generalizes well as long as there's a geometry where the optimum it converges to is flat and the stochastic gradients are well-behaved." Note though that the result does not explain why SGD would satisfy these properties.
11/
11/
One possible takeaway is that one should run SGD with a parametrization that makes these quantities small. A caveat is that the key quantities are not directly observable as they depend on test data.
12/
12/
The analysis is based on the information-theoretic techniques of Russo & Zhou (2016) and Xu & Raginsky (2017) that bounds the generalization error of any algorithm in terms of the mutual information between its input and output.
13/
13/
The twist is to apply it to a randomly perturbed version of the output of SGD and explicitly account for the mismatch between the perturbed and the original version.
14/
14/
The mutual information between the input and the perturbed output can then be bounded using a technique pioneered by Pensia, Jog & Loh (2017) for analyzing stochastic gradient Langevin dynamics.
15/
15/
The main innovation is that our perturbations *only exist in the analysis*, which gives us the flexibility of choosing them arbitrarily without affecting the actual performance of SGD. This enables adaptivity to parametrization, etc.
16/
16/
While the generalization bounds for SGLD are generally better, tuning its hyperparameters to trade off the training and generalization errors is much harder (especially when also allowing non-isotropic noise).
17/
17/
If you're interested to learn more, check out the paper on arxiv:
https://arxiv.org/abs/2102.00931
I'm very curious what you all think, especially since I don't consider myself an expert in the area. I'd particularly appreciate pointers to relevant literature that I have missed.
18/
https://arxiv.org/abs/2102.00931
I'm very curious what you all think, especially since I don't consider myself an expert in the area. I'd particularly appreciate pointers to relevant literature that I have missed.
18/
Special thanks to @lugosi_gabor for his help while preparing this paper!
Also, apologies for the bad drawings and handwriting in this thread. My PR budget couldn't afford HD images of purebred nonconvex loss surfaces this time.
19/FIN
Also, apologies for the bad drawings and handwriting in this thread. My PR budget couldn't afford HD images of purebred nonconvex loss surfaces this time.
19/FIN

 Read on Twitter
Read on Twitter