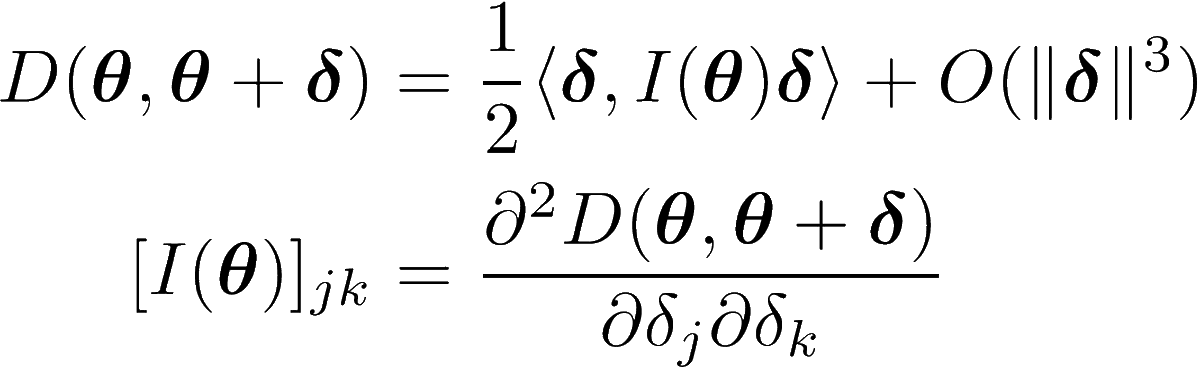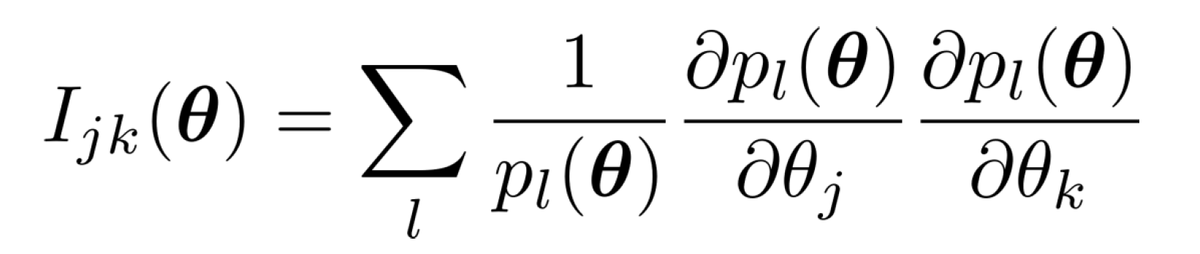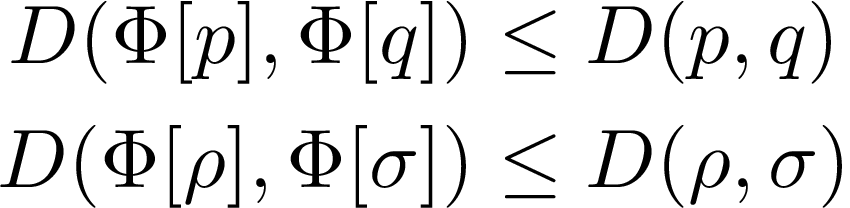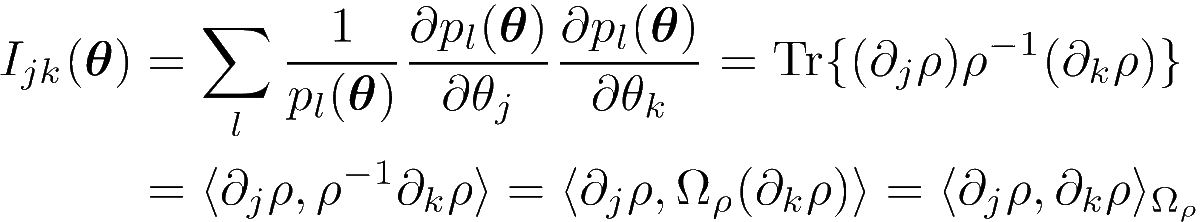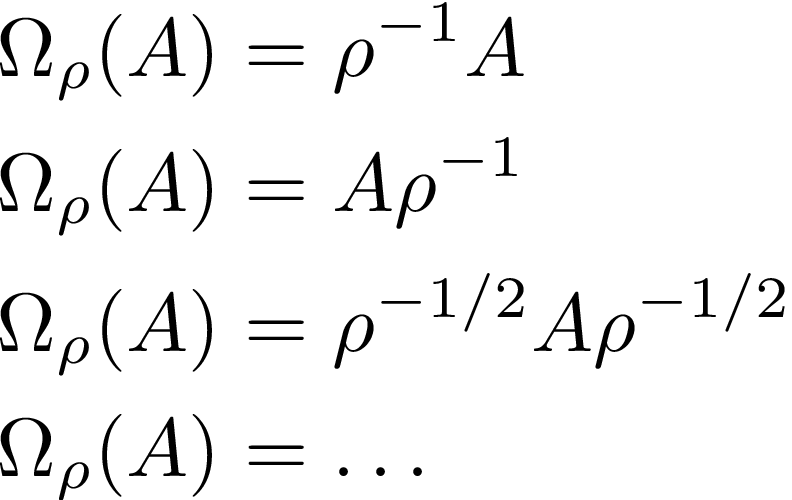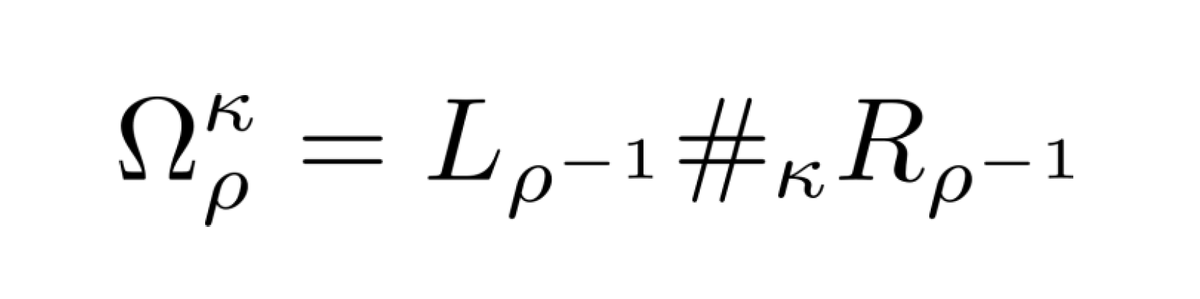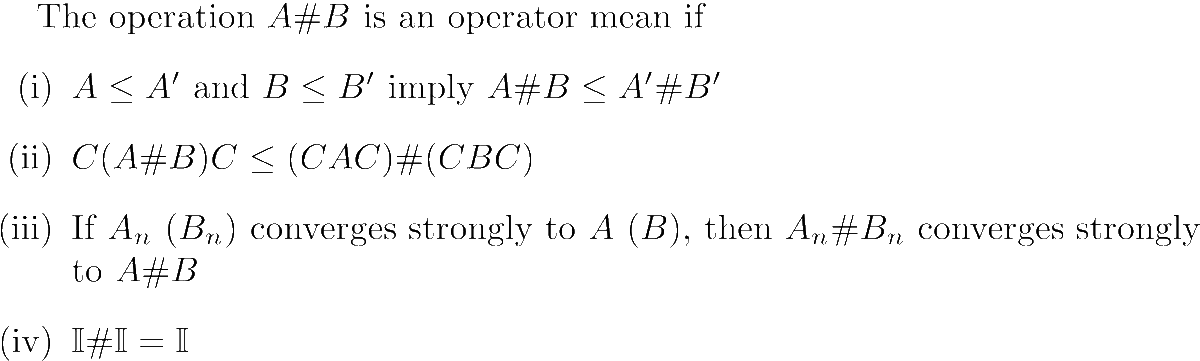I gave a short sneak-peek talk about quantum information geometry and monotone metrics today and thought I'd also share it here!

You might have heard about the Fisher information, both in a classical and quantum context, and there is actually a lot of interesting theory behind!

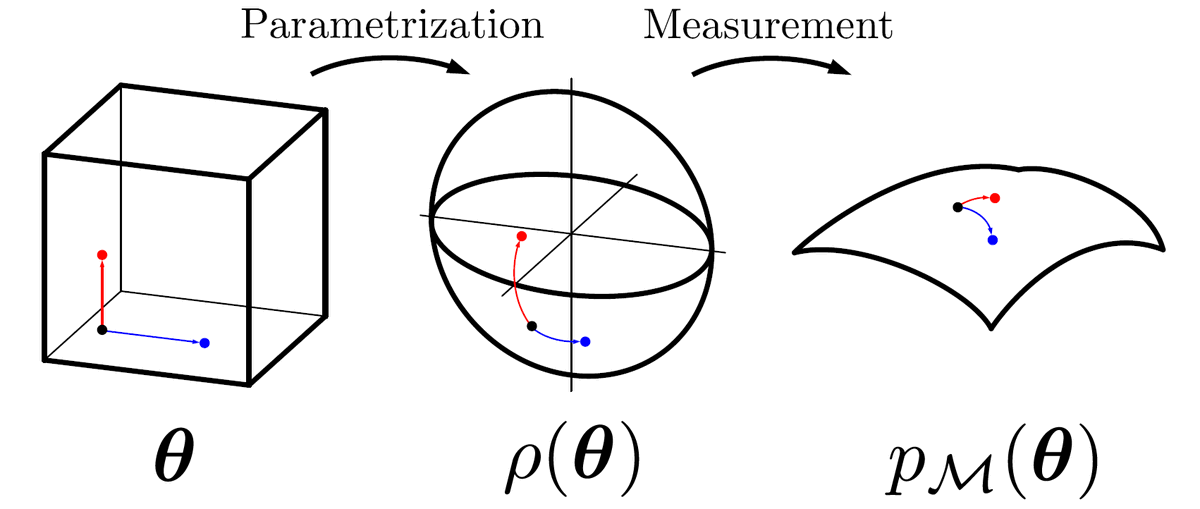
First, some motivation: if we use a parametrized state (or probability distribution), then it makes sense to measure distances between parameters by measuring the distances of the related states (or distributions), say by their fidelity. This is a "pullback" of the distance.

This is essentially a way of measuring distances between parameters that is informed by the actual thing you are parametrizing. By performing a Taylor expansion about a certain parameter, we can look at the local neighbourhood. The leading order will be second order.

Because 𝜹=0 is a minimum, 𝐼 will be positive semidefinite, and thus induces a scalar product. This is cool because it means we can now measure lengths of and angles between vectors in a way that is informed by the underlying distance measure!

Let's first look at the classical case, namely at the Kullback-Leibler divergence. If we do the expansion, we will find that 𝐼 is the (classical) Fisher information matrix. A very cool fact is that we would also get this result if we started with the fidelity distance!

This is due to a famous result by Morozova and Chentsov, which says that no matter which distance measure we pull back and expand, we will always end up with a multiple of the Fisher information matrix if the distance measure is monotonous, i.e. non-increasing under channels.

Now let's generalize to the quantum case. Instead of starting from quantum distance measures, it is more instructive to look at the Fisher information. We will first rewrite it in a way that looks more quantumly by replacing the distribution 𝑝 with a diagonal density matrix 𝜌.

We introduced a new scalar product, this time induced by an operator 𝛺 that "divides by 𝜌" – and here is where the quantum complications come in. In the classical case, everything commutes and there is only one way of dividing by 𝜌, but in the quantum case there are many!

In a very nice paper, Pétz showed that all those cases actually lead to different monotonous metrics, much contrary to the classical case. But we can nicely characterize them via operator means of left and right multiplication with the inverse of 𝜌!

Operator means generalize the classical notion of means (e.g. geometric or arithmetic) to operators. They were defined axiomatically by Kubo and Ando, onto whose work Pétz' is largely based. Examples are the arithmetic mean (A + B)/2 and the harmonic mean 2 (A⁻¹ + B⁻¹)⁻¹.

We have now seen that we can characterize all monotonous metrics in terms of operator means. This means we can exploit a lot of structure that is known about them but that I won't treat today. So let's go back to why we actually care about all those different monotonous metrics.

It's of course because they are super useful! Especially the SLD Quantum Fisher information, associated to the pullback of the fidelity, is widely used in metrology and other areas, mostly because fidelity is the "natural" way of measuring the similarity between quantum states.

But also many other monotonous metrics are used, we have the RLD Quantum Fisher information known from metrology, the Wigner-Yanase skew information or the Kubo-Mori information known from thermodynamics to name a few.

With the approach put forward by Pétz we have a way to put all of these different information measures under the same umbrella. That's it for today, I hope you learned something!