Read on Twitter
El hilo de hoy va a ser un poco distinto, esta vez no tendrá ningún relato histórico jugoso
Hoy, en la Nave de #MatesEnDomingo
, hablaremos de por qué es importante saber de estadística para que gente como Iker Jiménez no te engañe con el cambio climático
Dentro hilo
Hoy, en la Nave de #MatesEnDomingo
, hablaremos de por qué es importante saber de estadística para que gente como Iker Jiménez no te engañe con el cambio climáticoDentro hilo
DISCLAIMER:
Este hilo irá de estadística, de la importancia de entender la media pero también una cosa llamada varianza, pero no soy experto en cambio climático
Para eso, el vídeo de @QuantumFracture y seguir a @pablorros_ @dr_xeo @AndreuEscriva
Este hilo irá de estadística, de la importancia de entender la media pero también una cosa llamada varianza, pero no soy experto en cambio climático
Para eso, el vídeo de @QuantumFracture y seguir a @pablorros_ @dr_xeo @AndreuEscriva
Estos días hubo polémica por un tuit de Iker en el que, amén de confundir clima con meteorología y de poner una foto pillada de internet de hace años que no correspondía con lo que decía, hablaba de «calentamiento global», e insinuaba que bueno, hace frío, pa tanto no será, ¿no?
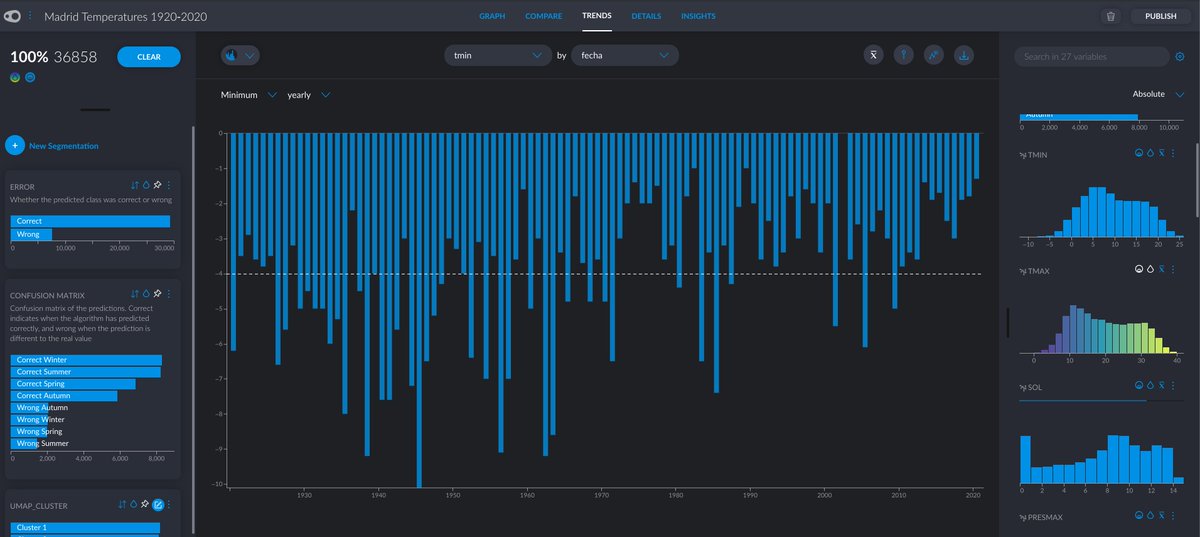
Una parte de las consecuencias del cambio climático es que la temperatura media ha aumentado de forma significativa en los últimos años (puedes ver aquí las temperaturas de los inviernos en Madrid de @victorianoi)
PERO
¿Solo importa la temperatura media?
PERO
¿Solo importa la temperatura media?
¿No existen otras formas de medir cómo se CONCENTRAN los datos?
CHORPRECHA: sí, existen, y las famosas son las 3M (medidas de CENTRALIZACIÓN, media, moda y mediana)
¿Cuál es la diferencia entre ellas? Bebo café me lamento por no saborearlo por el covid, y sigo 
CHORPRECHA: sí, existen, y las famosas son las 3M (medidas de CENTRALIZACIÓN, media, moda y mediana)
¿Cuál es la diferencia entre ellas? Bebo café
me lamento por no saborearlo por el covid, y sigo
Empecemos por lo fácil
¿Qué es la media (aritmética)?
Esta seguro que te la sabes porque la usas a diario cuando vas a comer con gente (los que...saboreáis la comida):
1) sumo los valores (por ejemplo, 10+15+20 = 35)
2) divido entre el número de cosas sumadas (35/3 = 15)
¿Qué es la media (aritmética)?
Esta seguro que te la sabes porque la usas a diario cuando vas a comer con gente (los que...saboreáis la comida
):1) sumo los valores (por ejemplo, 10+15+20 = 35)
2) divido entre el número de cosas sumadas (35/3 = 15)
La media es lo que llamamos MEDIDA DE CENTRALIZACIÓN: en torno a qué valor se concentran los datos
Su principal ventaja es que la conoces, es fácil. Pero no es la única
Otra es la MEDIANA, y básicamente consiste en establecer un orden
Su principal ventaja es que la conoces, es fácil. Pero no es la única
Otra es la MEDIANA, y básicamente consiste en establecer un orden
Ejemplo: si tienes 9 cartas 1,2,3,4 - 5 - 6,7,8,9, la mediana sería el 5. ¿Por qué? Porque está en medio. Chinpún
Y la última, la más estilosa: la MODA, «lo trending», lo más repetido
La moda de, por ej., edades de amigos (31, 30, 30, 27, 30, 25, 30) es la más repetida: 30
Y la última, la más estilosa: la MODA, «lo trending», lo más repetido
La moda de, por ej., edades de amigos (31, 30, 30, 27, 30, 25, 30) es la más repetida: 30
Aunque no se suele usar en estadística ya que su manejo (por ejemplo, para una regresión) es bastante complicado, siempre que veas un diagrama de barras, es la barrita más alta
Bien, ya sabemos que existe algo más que la media, nuestras amigas las MEDIDAS DE CENTRALIZACIÓN
PEEEERO....¿PARA QUÉ?
¿Por qué no usamos siempre la media?
Respuesta corta: porque no somos periodistas
Respuesta menos corta
PEEEERO....¿PARA QUÉ?
¿Por qué no usamos siempre la media?
Respuesta corta: porque no somos periodistas
Respuesta menos corta
Aunque la media sea la más conocida, y la más usada, la mayoría de veces se usa mal, ya que la media SOLO nos da información real cuando lo que medimos es SIMÉTRICO, cuando hay valores similares por arriba y por abajo
¿Qué sucede cuando no? Pues que ...se comporta raruno
¿Qué sucede cuando no? Pues que ...se comporta raruno
Imagina que tienes 10 cartas iguales, todas son un 1. La media sería por tanto...eso, 1
¿Pero qué sucedería si añadimos una carta que sea un 12?
(1+1+1+1+1+1+1+1+1+1+12) / 11 = 2
¡La media se ha duplicado, pero solo ha cambiado el 9.09% de los datos!
¿Pero qué sucedería si añadimos una carta que sea un 12?
(1+1+1+1+1+1+1+1+1+1+12) / 11 = 2
¡La media se ha duplicado, pero solo ha cambiado el 9.09% de los datos!
Y esta es la principal desventaja de la media, que si los valores no están bien repartidos y aparecen valores atípicos (como ese 12), lo que nos muestra puede distar mucho de la realidad (decimos que la media NO ES ROBUSTA)
¿Dónde se usa esta trampita?
¿Dónde se usa esta trampita?
Esta poca robustez de la media se usa de forma constante en medios cuando quieren hablar de salarios, una variable que por desgracia no es simétrica: mucha gente cobrando mierda, poca gente siendo Amancio
Esa asimetría hace que el salario medio no refleje bien la realidad
Esa asimetría hace que el salario medio no refleje bien la realidad
Bien, ¿esto qué cojones tiene que ver con el chupacabras de Iker Jiménez?
Iker usa el hecho de que esté nevando para insinuar que, como hace frío, pues eso implica que no hay lo que el llama el calentamiento global.
En primer lugar esa mentira: SÍ ESTÁ SUBIENDO
Iker usa el hecho de que esté nevando para insinuar que, como hace frío, pues eso implica que no hay lo que el llama el calentamiento global.
En primer lugar esa mentira: SÍ ESTÁ SUBIENDO
Y sí, obviamente que haya subido no implicaría automáticamente una causalidad (porque correlación no implica causalidad, pero eso en otro hilo), pero como cuenta muy bien Crespo en el vídeo, es que además conocemos suficientemente bien los mecanismos de esa subida.
No es solo que insinúe algo falso
El error es usar solo el término «calentamiento global», ya que alude solo a una de nuestras medidas de centralización: el incremento de temperatura media
¿Es solo cuestión de media el CAMBIO climático?
CHEÑORES/AS, hablemos de la varianza
El error es usar solo el término «calentamiento global», ya que alude solo a una de nuestras medidas de centralización: el incremento de temperatura media
¿Es solo cuestión de media el CAMBIO climático?
CHEÑORES/AS, hablemos de la varianza
Y es que en estadística, ninguna medida de centralización nos da por sí misma suficiente información: sabemos el valor en torno al que se concentran pero...
¿Cómo se concentran? ¿Están muy pegados a ese valor? ¿O hay valores muy alejados por arriba y muy alejados por abajo?
¿Cómo se concentran? ¿Están muy pegados a ese valor? ¿O hay valores muy alejados por arriba y muy alejados por abajo?
Hablemos pues de otras amigas: las medidas de DISPERSIÓN
¿Cómo medir cuánto se dispersan los datos respecto a ese centro?
Supongamos el salario de 3 meses que te han ido distinto: 2000€, 0€ y -2000€ (para nada basado en hechos reales)
Tomemos la media como centro 0 euros
¿Cómo medir cuánto se dispersan los datos respecto a ese centro?
Supongamos el salario de 3 meses que te han ido distinto: 2000€, 0€ y -2000€ (para nada basado en hechos reales
)Tomemos la media como centro 0 euros
Una primera tentación para medir esa «distancia» es simplemente restar, ¿no?
2000-0 = 2000€
0 - 0 = 0€
-2000-0 = -2000€
¿Problema?
Al hacer el promedio de esas desviaciones pues...¡vuelve a dar 0!
Tenemos una dispersión que no distingue (-2000, 0, 2000) de (0, 0, 0).
2000-0 = 2000€
0 - 0 = 0€
-2000-0 = -2000€
¿Problema?
Al hacer el promedio de esas desviaciones pues...¡vuelve a dar 0!
Tenemos una dispersión que no distingue (-2000, 0, 2000) de (0, 0, 0).
Esto sucede porque los signos positivos y negativos se están cancelando
¿Cómo evitarlo?
La idea más simple para eliminar signos es elevar al cuadrado:
(2000-0)² = 4 000 000
(0-0)² = 0
(-2000-0)² = 4 000 000
Bien, ya no tenemos signos que se cancelen, podemos sumar y promediar
¿Cómo evitarlo?
La idea más simple para eliminar signos es elevar al cuadrado:
(2000-0)² = 4 000 000
(0-0)² = 0
(-2000-0)² = 4 000 000
Bien, ya no tenemos signos que se cancelen, podemos sumar y promediar
Así que podemos
1) calcular lo que se desvía cada dato respecto a la media
2) Elevar esa desviación al cuadrado para eliminar signos
3) Hacer el promedio de esas desviaciones
Promedio = (4 000 000 + 0 + 4 000 000) / 3 = 2 666 667
Amigos/as, os presento a la famosa VARIANZA
1) calcular lo que se desvía cada dato respecto a la media
2) Elevar esa desviación al cuadrado para eliminar signos
3) Hacer el promedio de esas desviaciones
Promedio = (4 000 000 + 0 + 4 000 000) / 3 = 2 666 667
Amigos/as, os presento a la famosa VARIANZA
La VARIANZA es una medida de DISPERSIÓN que es, ni más ni menos, que el promedio de las desviaciones al cuadrado (para eliminar esos signos).
A igual conjunto de datos, si crece la varianza ==> los datos están más dispersos
Si decrece ==> más junticos entorno al centro
A igual conjunto de datos, si crece la varianza ==> los datos están más dispersos
Si decrece ==> más junticos entorno al centro
PERO
Habemus un problema: si mido estaturas de personas y quiero dar la dispersión, al medir las estaturas en metros y elevarlas al cuadrado...
¡La dispersión será de...5m²! No tiene mucho sentido tratar a las personas como baldosas, ¿no crees?
Habemus un problema: si mido estaturas de personas y quiero dar la dispersión, al medir las estaturas en metros y elevarlas al cuadrado...
¡La dispersión será de...5m²! No tiene mucho sentido tratar a las personas como baldosas, ¿no crees?
Como a veces necesitamos una medida de dispersión en las unidades de los datos, se puede simplemente calcular la varianza y tras tenerla, hacerle la raíz cuadrada para eliminar ese ²
Esto es lo que llamamos DESVIACIÓN TÍPICA, en las unidades de los datos (seguimos)
Esto es lo que llamamos DESVIACIÓN TÍPICA, en las unidades de los datos (seguimos
)
PERO...TENEMOS OTRO PUTO PROBLEMA
Si yo mido pinos y virus, uno en metros y el otro en nanómetros, ¿cómo puedo saber cuál de mis muestras es más dispersa?
Lo que ocurrirá es que la desv. típica será más alta en pinos que en virus (¡metros vs nanómetros!): no son comparables
Si yo mido pinos y virus, uno en metros y el otro en nanómetros, ¿cómo puedo saber cuál de mis muestras es más dispersa?
Lo que ocurrirá es que la desv. típica será más alta en pinos que en virus (¡metros vs nanómetros!): no son comparables
Lo que podemos hacer es convertir esa desv. típica en algo ADIMENSIONAL, dando igual si mides metros, nanómetros, kilos o pascales.
Y la opción más sencilla es dividir esa desviación entre la media: os presento a la última medida de dispersión, el COEFICIENTE DE VARIACIÓN
Y la opción más sencilla es dividir esa desviación entre la media: os presento a la última medida de dispersión, el COEFICIENTE DE VARIACIÓN
Esa tres medidas son las que usan de forma constante en estadística para no solo dar una estimación, un valor, sino construir incertidumbre, algo que nos permita saber por dónde rondará el dato aprox.
Y ESO ES EL CAMBIO CLIMÁTICO: dispersión fuera de lo normal
Y ESO ES EL CAMBIO CLIMÁTICO: dispersión fuera de lo normal
El problema del cambio climático no es solo un aumento de las medidas de centralización (temperatura media, por ejemplo) sino un aumento enorme de la variabilidad
¿Y cómo medimos lo variado que es algo en matemáticas? Efectivamente, con las medidas de dispersión
¿Y cómo medimos lo variado que es algo en matemáticas? Efectivamente, con las medidas de dispersión
El problema del cambio climático no es solo que la temperatura sea más alta en algunos sitios o más baja en otros, el problema es que las variaciones de temperatura y otras variables han subido su varianza, mucho más de lo que nuestro ecosistema puede asimilar en tan poco tiempo
¿Cómo detectar gráficamente cuando sucede?
Este gráfico nos muestra una nube de datos donde...no sube nada: todos los valores se mantienen más o menos en torno a un nivel y dentro de una franja cuya altura no cambia
Este gráfico nos muestra una nube de datos donde...no sube nada: todos los valores se mantienen más o menos en torno a un nivel y dentro de una franja cuya altura no cambia
Sin embargo este gráfico nos muestra una nube de puntos donde la MEDIA se incrementa con el paso del tiempo (los puntos van subiendo según avanzamos en el eje horizontal)
PERO
no aumenta la varianza (dispersión): todos los puntos siguen en una franja de anchura fija
PERO
no aumenta la varianza (dispersión): todos los puntos siguen en una franja de anchura fija
Es en este gráfico donde no solo tenemos una subida de la media sino que además vemos como los datos varían mucho más, tienen más saltos, son más dispersos ya que la franja va aumentando de tamaño: cada vez las subidas y bajadas son más amplias (amplitud térmica, ¿te suena?)
Como decía, podría haberme pegado la paliza de buscar información sobre la parte más técnica del cambio climático, pero me conformo con que hayas entendido la diferencia entre centralización y dispersión, y su gran gran utilidad :)
La parte técnica se la dejo a los expertos :)
La parte técnica se la dejo a los expertos :)
Espero que te haya servido para entender cosas que quizás diste como la varianza o la mediana, y saber por qué se definen así y su utilidad para no ser engañados, y si es así RT se agradece :)
Nos vemos en el próximo #MatesEnDomingo
Más divulgación: https://www.instagram.com/javieralvarezliebana/
Nos vemos en el próximo #MatesEnDomingo
Más divulgación: https://www.instagram.com/javieralvarezliebana/
Sobre varianza y aumento de la variabilidad (ergo de fenómenos extremos), os dejo en el hilo esta maravilla de gráfica https://twitter.com/LostTransposon/status/1347494519764357122
