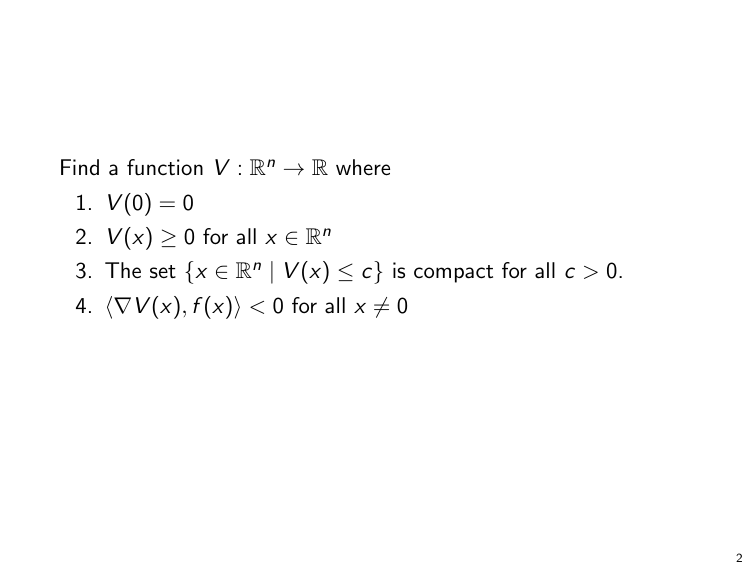I’m having an especially hard time concentrating on research this week, but instead of doomscrolling on twitter I guess I’ll do something semi-productive and make another twitter thread.

Today's topic: What is a Lyapunov function? 1/

I'm going to assume some (not a lot) working knowledge of ODE's.
@3blue1brown's excellent video on differential equations should cover everything we need



2/

We begin with the notion of stability. Given an ODE ẋ = f(x), a point x* where f(x*) = 0 is called an equilibrium. This is because any solution starting at x* will remain at x* for all time. 3/

We call x* Lyapunov stable if any solution starting near x* remains near x* for all time. We say x* is asymptotically stable, if in addition, all solutions beginning near x* converge to x*. (All of this can be formalized with ϵ's and δ's but I won't do that here) 4/

Our goal is simple: Suppose that x* is an equilibrium of the ODE, ẋ = f(x). How can we show that x* is asymptotically stable? Ideally we would like to this without solving the ODE, using only our knowledge of the geometry of the vector field f(x). 5/

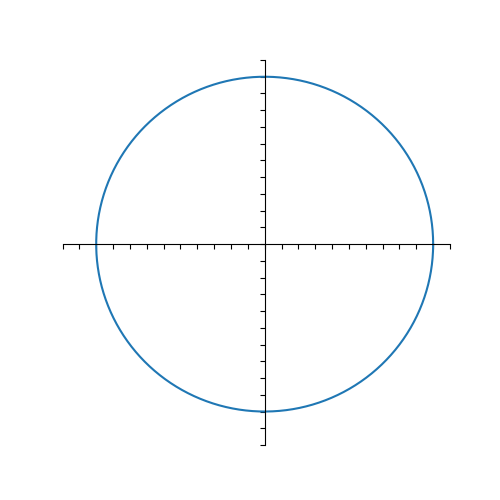
I’m going to simplify things a bit by assuming that x*=0. Lets recall some geometry. The circle of radius c is precisely the set of points x such that |x| = c. We can think of the circle as a level set of the function V(x) = |x|. 6/

Any point, p1, that is on the circle has distance c to the origin. If p2 is inside the circle, its distance to the origin is <c. Likewise if p3 is outside the circle, its distance to the origin is >c. 7/

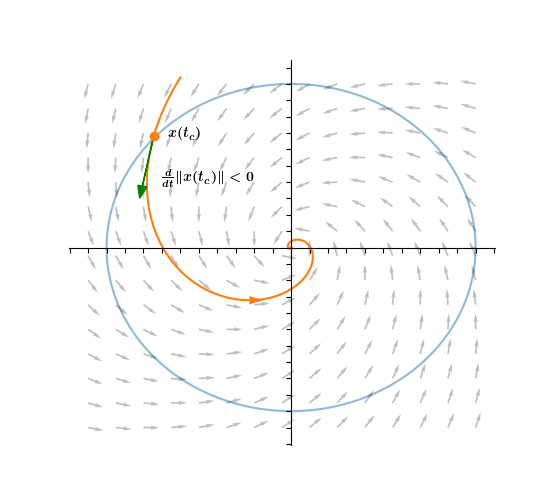
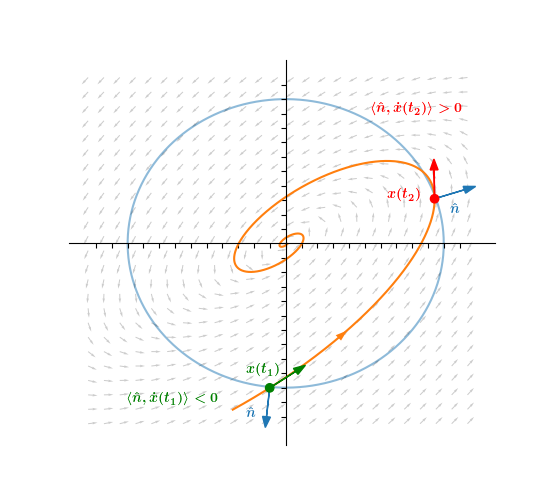
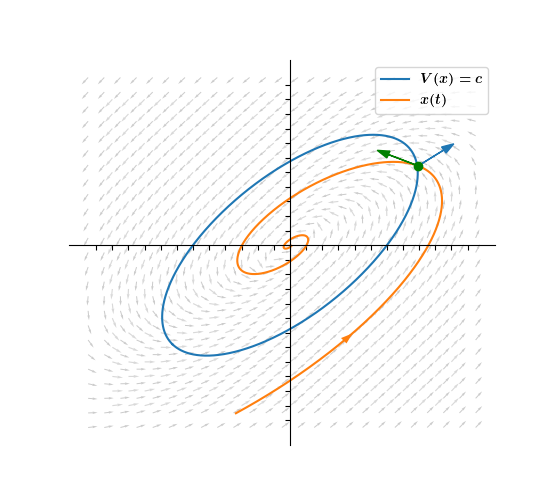
We now superimpose the circle onto the phase portrait of the ODE and highlight a specific solution, x(t). Since |x(t1)| < c and |x(t2)| > c, we know by the mean value theorem that the derivative of |x(t)| must be negative at some time in the interval [t1, t2]. 8/

In fact, d/dt |x(tc)| < 0 where tc is the time at which x(t) intersects the circle. This is because the vector tangent to the solution points INSIDE the circle, so |x(t)| must be decreasing when t=tc. 9/

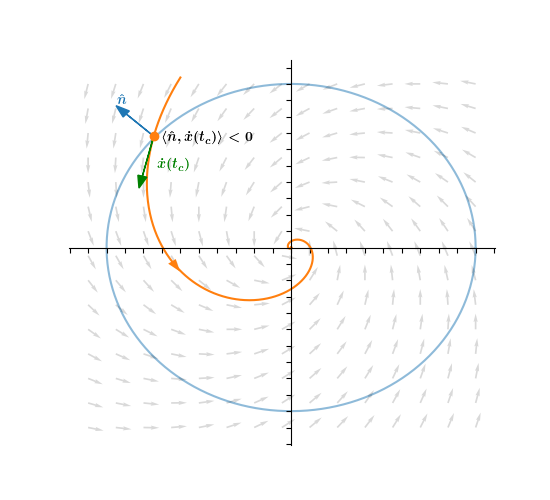
How do we know that the tangent points inside the circle? Easy! The tangent to x(tc) is ẋ(tc). If the inner product of ẋ(tc) with the outward normal vector to the circle, n̂, is negative, then the angle between the vectors is > 90∘, which means ẋ(tc) points inside. 10/

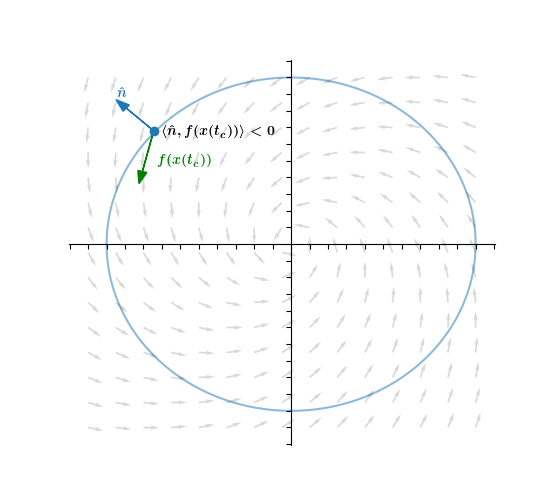
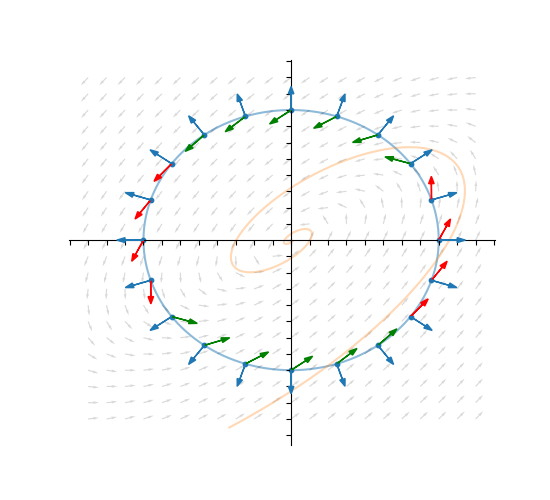
But since x(t) is a solution to the ODE, ẋ(tc)=f(x(tc)). This means to determine whether |x(tc)| is decreasing we don't actually need to know the whole trajectory x(t). All we need to look at is the angle between the vector field and the outward normal at that point 11/

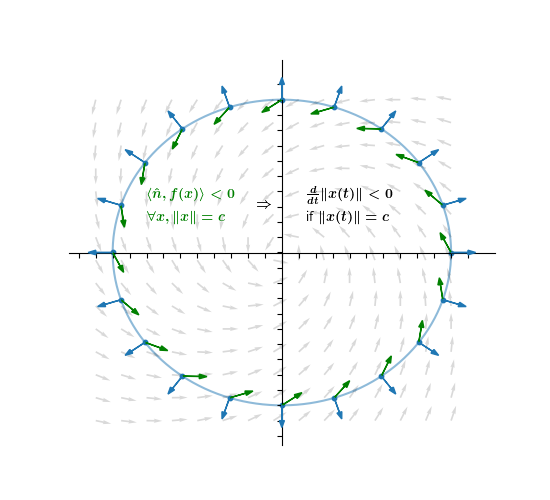
In fact, if ⟨n̂, f(x)⟩ < 0 for all points x that are on the circle, then we know that for EVERY solution that intersects the circle, |x(t)| is decreasing at the point of intersection. 12/

This leads to our first test of convergence, which I will call the "circle test". If ⟨n̂, f(x)⟩ < 0 for all points x ≠ 0, then every solution to the ODE ẋ=f(x) converges to the origin. Here n̂ refers to the outward normal vector to the circle that intersects x. 13/

If f(x) passes the circle test, then |x(t)| decreases monotonically along all solutions, and converges to zero! Take a moment to appreciate this: we made a statement about every solution to the ODE without ever solving it, using only the properties of f(x)! 14/

Of course while the circle test is clearly sufficient for convergence, it is not necessary. Consider the following vector field. By visual inspection, we can convince ourselves that all solutions converge to the origin, but the circle test fails! 15/

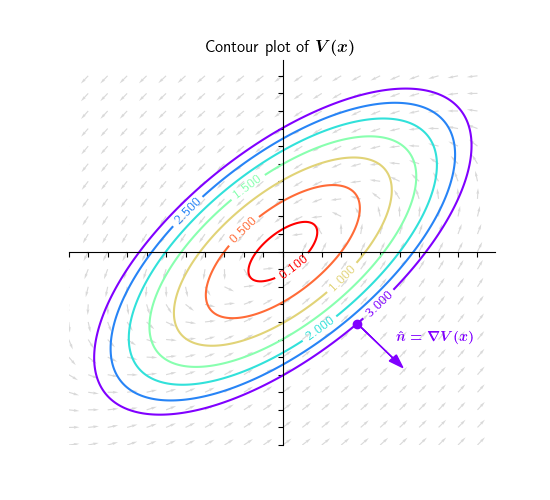
Fear not, the situation isn't hopeless! Remember the circle is the level set of the function V(x)=|x|. Perhaps we can replace V with another function which captures some notion of "distance", and repeat the above procedure with the level sets of this new V. 16/

In order for V to be valid notion of distance it should satisfy the following properties. The first two properties, I hope, are clear: the distance of the origin to itself is 0, and every point has non-negative distance to the origin. 17/

The third property basically says every point x should have finite distance to the origin. It is mostly there for technical reasons, to ensure that the statements we make hold globally 18/

We want to do the same thing as above, replacing circles with level sets of V. To do this we need to know how to compute the outward normal vector. You might remember from multivariable calculus that the outward normal to the level set is simply the gradient vector ∇V(x) 19/

Ok so the game is now as follows: Find some function V satisfying the 3 properties outlined earlier such that ⟨∇V(x), f(x)⟩ < 0 for all x ≠ 0. This ensures that d/dt V(x(t)) < 0, so V decreases monotonically along all solutions, and all solutions converge to the origin 20/

Such a function, if it can be found, is called a Lyapunov function. The existence of a Lyapunov function (as defined here) guarantees that the origin is globally asymptotically stable! 21/

Some remarks: 1. Some of you might have noticed that I began by introducing asymptotic stability, but in the examples I only discussed global attractivity. Asymptotic stability is stronger than attractivity, but both are guaranteed by Lyapunov theory 22/

2. Finding a Lyapunov function is, in general, a nontrivial task. As far as I know there is no general method for constructing Lyapunov functions for nonlinear ODEs. It really is more of an art than a science. 23/

3. Lyapunov theory is extremely powerful and there are numerous generalizations in the literature (eg. ISS-Lyapunov functions, control Lyapunov functions, barrier functions, etc.) I'll probably do a follow up thread discussing some of these. 24/

4. Lyapunov functions aren't just for analysis, they also a useful DESIGN tool. For example, given a dynamical system with inputs, ẋ = f(x, u), we can use (control) Lyapunov functions to construct a feedback controller stabilizing the state to the origin. 25/

Thats all for now! Please give me feedback or let me know of topics that I should discuss!

It seems that not many people do threads like these on topics in control theory, so I'll do few more on foundational ideas before moving on to more cutting edge stuff. 26/26.