𝗧𝗛𝗥𝗘𝗔𝗗 
Ever wonder why π takes the specific value it does?
Well … this thread isn’t about that. Instead, I’ll discuss other values that “pi” might take. Spoiler: it can be anything in the interval [3,4]. It's my first time writing a thread, so I hope y’all enjoy! (1/32)

Ever wonder why π takes the specific value it does?
Well … this thread isn’t about that. Instead, I’ll discuss other values that “pi” might take. Spoiler: it can be anything in the interval [3,4]. It's my first time writing a thread, so I hope y’all enjoy! (1/32)
I'll use some notions of vectors and metric spaces. If you don’t know what those are, I encourage you to check out these great expositions by Cornelia Van Cott, which were my initiation into the topic. (2/32)
An article: https://www.maa.org/sites/default/files/pdf/Mathhorizons/pdfs/mh-vancott.pdf
A talk:
An article: https://www.maa.org/sites/default/files/pdf/Mathhorizons/pdfs/mh-vancott.pdf
A talk:
First, we set the scene. The plane ℝ² is a vector space (over ℝ), meaning that it comes equipped with two (compatible) operations: addition and scaling (both happen component-wise). A norm on ℝ² is a notion of distance that is compatible with these two operations. (3/32)
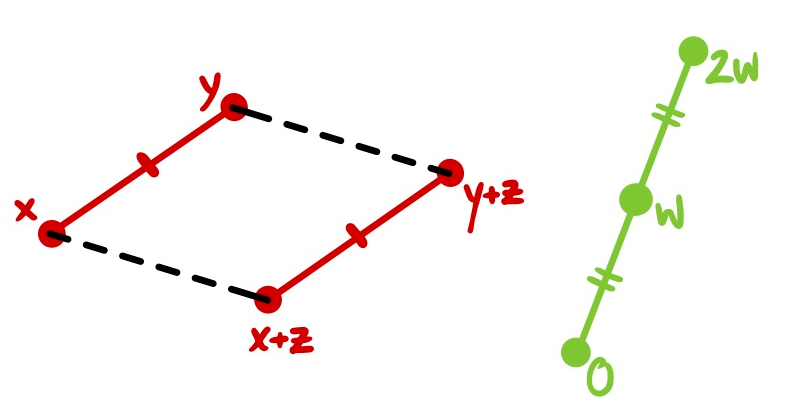
More precisely, a norm is a metric d such that: d(x,y)=d(x+z,y+z) (translation) and r*d(x,y)=d(rx,ry) (scaling) for any vectors x,y,z and scalar r>0. Since a norm is translation-invariant, it can also be given just by distance to the origin, which I write ᵈ||x||=d(x,0). (4/32)
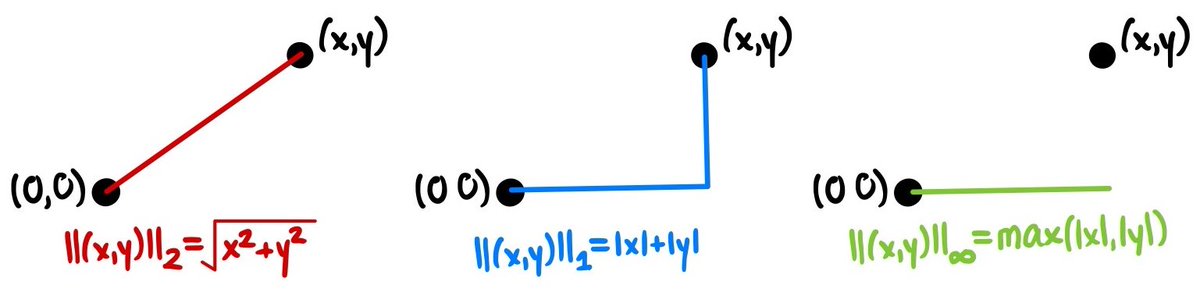
The most commonly used norm on ℝ² is
||(x,y)||=√(x²+y²). This has the special property that it comes from an inner product! Other examples include the
“taxicab” norm ||(x,y)||=|x|+|y|, and the
“sup” norm ||(x,y)||=max(|x|,|y|). (The single bars denote absolute value.) (5/32)
||(x,y)||=√(x²+y²). This has the special property that it comes from an inner product! Other examples include the
“taxicab” norm ||(x,y)||=|x|+|y|, and the
“sup” norm ||(x,y)||=max(|x|,|y|). (The single bars denote absolute value.) (5/32)
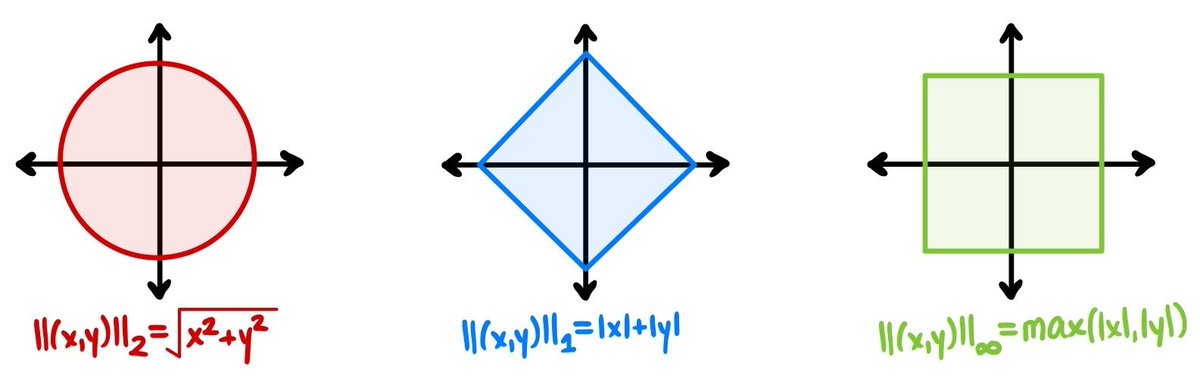
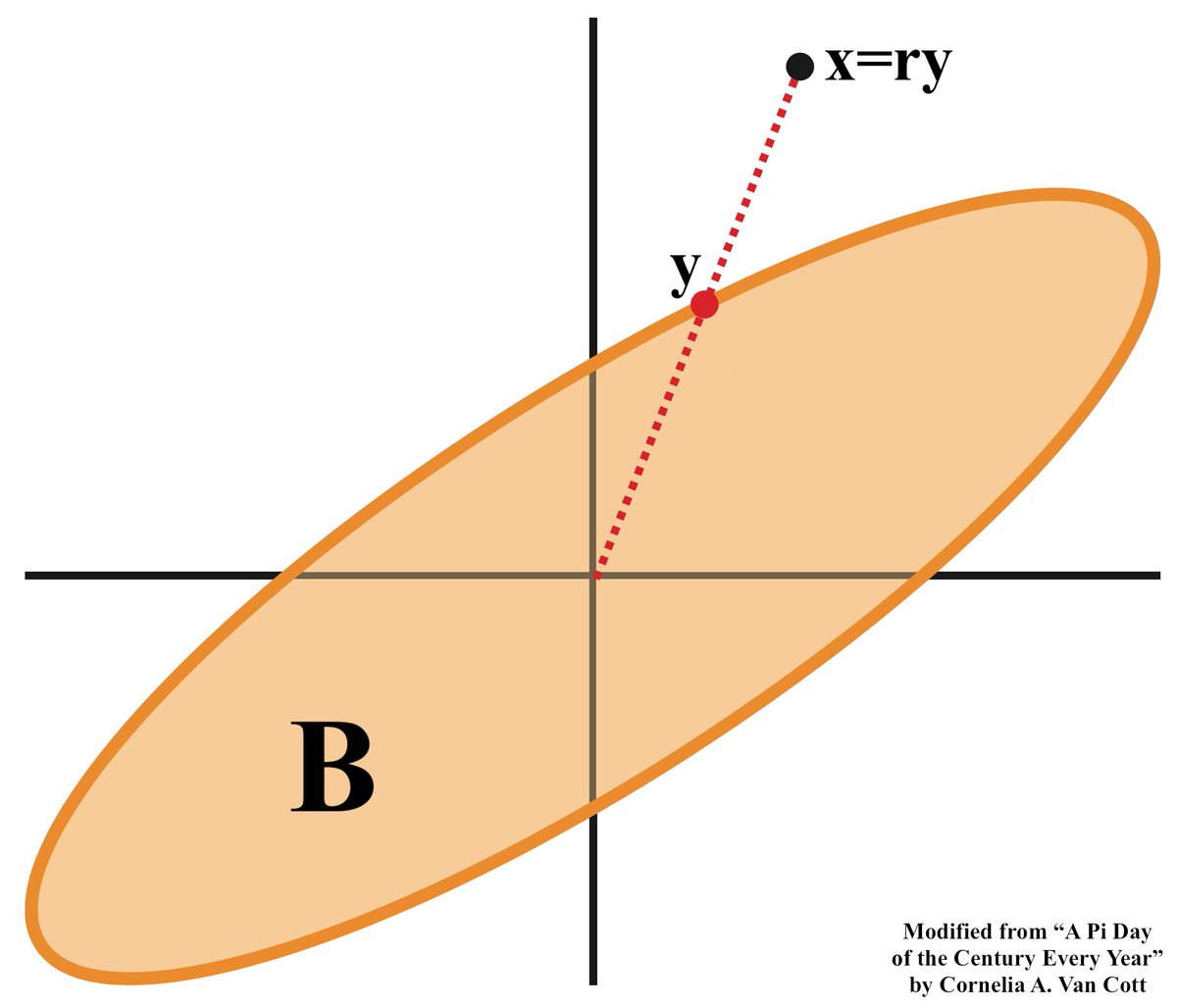
To see what the norms “look like,” it is useful to look at disks & circles. The disk of radius r>0 centered at y is Bᵈ(y,r)={x:d(x,y)≤r}. The circle is its boundary ∂Bᵈ(y,r)={x:d(x,y)=r}. But really, we only need the unit disk centered at 0, which I call Bᵈ=Bᵈ(0,1). (6/32)
Any other disk is similar to Bᵈ, by the translation and scaling properties of the norm: Bᵈ(y,r)=Bᵈ(0,r)+y=r*Bᵈ+y. Thus Bᵈ is singled out as 1 representative of the ubiquitous “shape of any disk” under our norm d. In fact, we can discern the norm d entirely from Bᵈ. (7/32)
The disk Bᵈ of a norm always contains a neighborhood of 0 and is convex, closed, bounded and symmetric about the origin. Conversely, if B is any subset of ℝ² with these properties, then B=Bᵈ for a unique norm d: let ᵈ||x|| be the unique r>0 such that x/r ∈ ∂B. … (8/32)
… In words, the length of x ∈ ℝ² is the unique value r≥0, such that x=ry for a unit vector y. The assumed properties of B ensure that we get a norm, so this gives a bijection between norms and such sets B. Understanding norms thus boils down to a study of these shapes. (9/32)
In particular, the shape of the unit circle ∂Bᵈ determines an analogue of pi. To discuss it, we first need to understand the meaning of “circumference.” Just as our norm defines the shortest distance between two points, we can measure the lengths of more curvy paths. (10/32)
Partitioning a path γ:[0,1]→ℝ² into finitely many steps 0=t₀≤t₁≤…≤tᵢ=1 affords us an "estimation” of its length:
d(γ(t₀),γ(t₁))+d(γ(t₁),γ(t₂))+…+d(γ(tᵢ₋₁),γ(tᵢ)).
But these points may miss some of the path’s curviness, giving too small a value. (11/32)
d(γ(t₀),γ(t₁))+d(γ(t₁),γ(t₂))+…+d(γ(tᵢ₋₁),γ(tᵢ)).
But these points may miss some of the path’s curviness, giving too small a value. (11/32)
Thus we define the length lenᵈ(γ) to be the supremum of the above approximating sum over all partitions 0=t₀≤t₁≤…≤tᵢ=1. This is always well-defined in [0,∞], but it may not be finite! For example, the snowflake fractal has infinite length: (12/32)
https://upload.wikimedia.org/wikipedia/commons/2/25/Kochsim2.gif
https://upload.wikimedia.org/wikipedia/commons/2/25/Kochsim2.gif
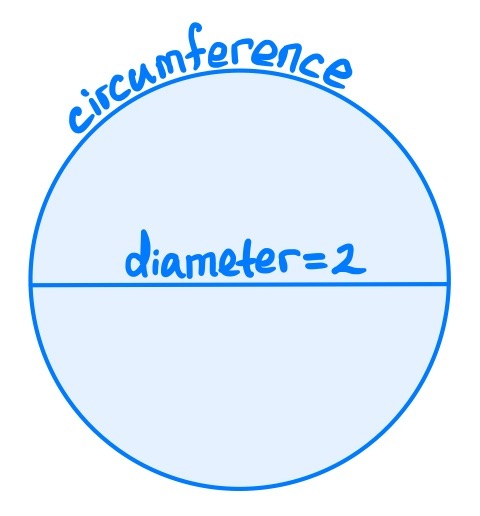
But for “nice” curves (e.g. smooth or bounding a convex region), we do always get a finite length. In particular, the length of the unit circle ∂Bᵈ is well-defined. Since the unit circle has diameter 2, we define pi to be circumference/diameter:
ϖ(d)=lenᵈ(∂Bᵈ)/2. (13/32)
ϖ(d)=lenᵈ(∂Bᵈ)/2. (13/32)
This weird symbol ϖ is a cursive variant of pi, which is used to distinguish from the classic constant π=3.1415….
The latter is actually given by π=ϖ(d), where
ᵈ||(x,y)||=√(x²+y²) is our first example from above (or d can be any norm coming from an inner product). (14/32)
The latter is actually given by π=ϖ(d), where
ᵈ||(x,y)||=√(x²+y²) is our first example from above (or d can be any norm coming from an inner product). (14/32)
Note that d occurs twice in the formula ϖ(d)=lenᵈ(∂Bᵈ)/2. We could make Bᵈ larger by scaling by some r>1, but the unit by which we measure length becomes larger by the same amount. These two factors cancel out in the sense that ϖ(r*d)=ϖ(d). So while it might seem … (15/32)
… that a bigger Bᵈ has a bigger circumference, we must remember that this is balanced by measuring length in terms of d. Thus, the value of ϖ(d) is much more about the “shape” of Bᵈ than the “size.” The next step is to calculate ϖ(d) for an important class of examples. (16/32)
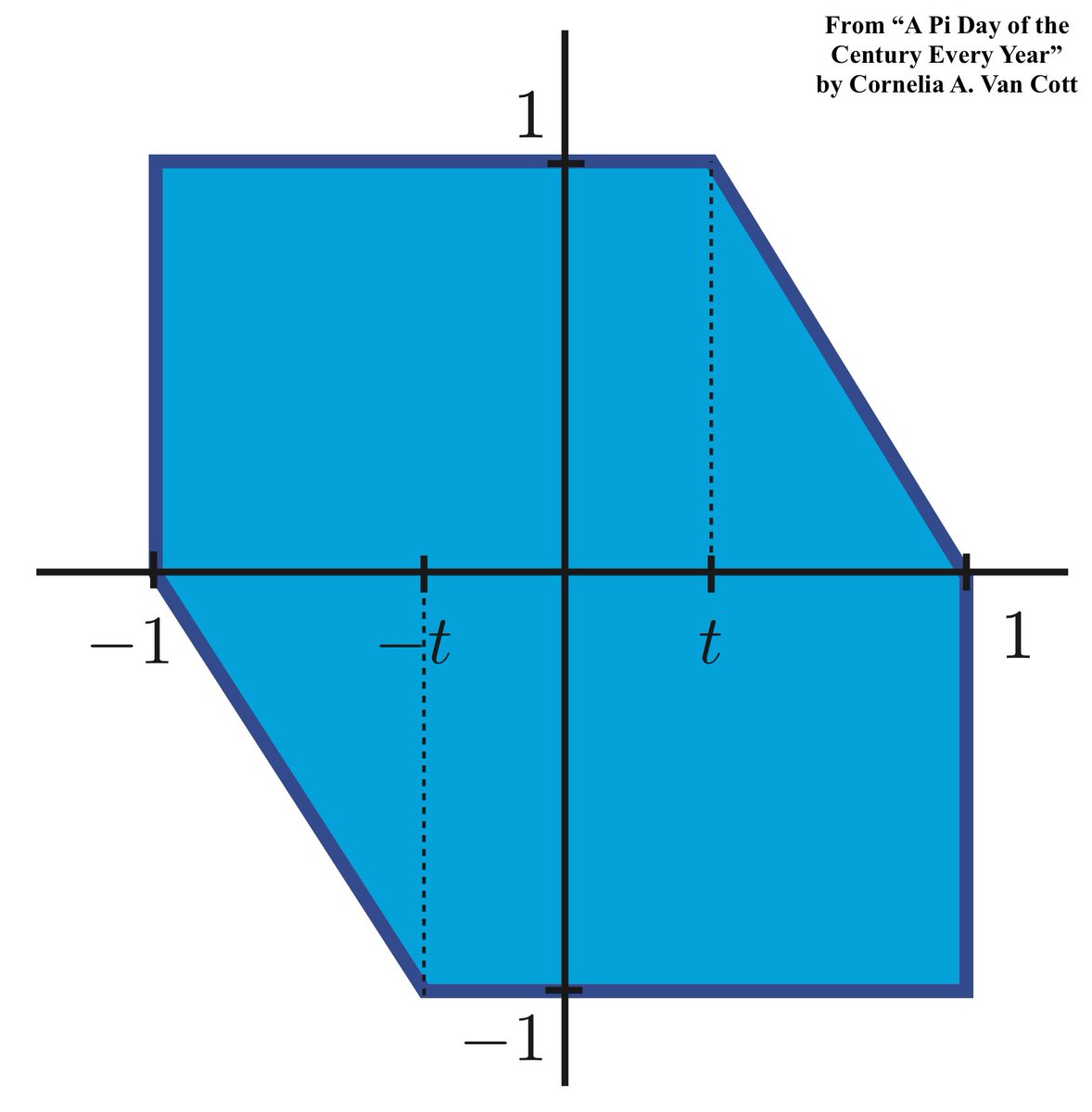
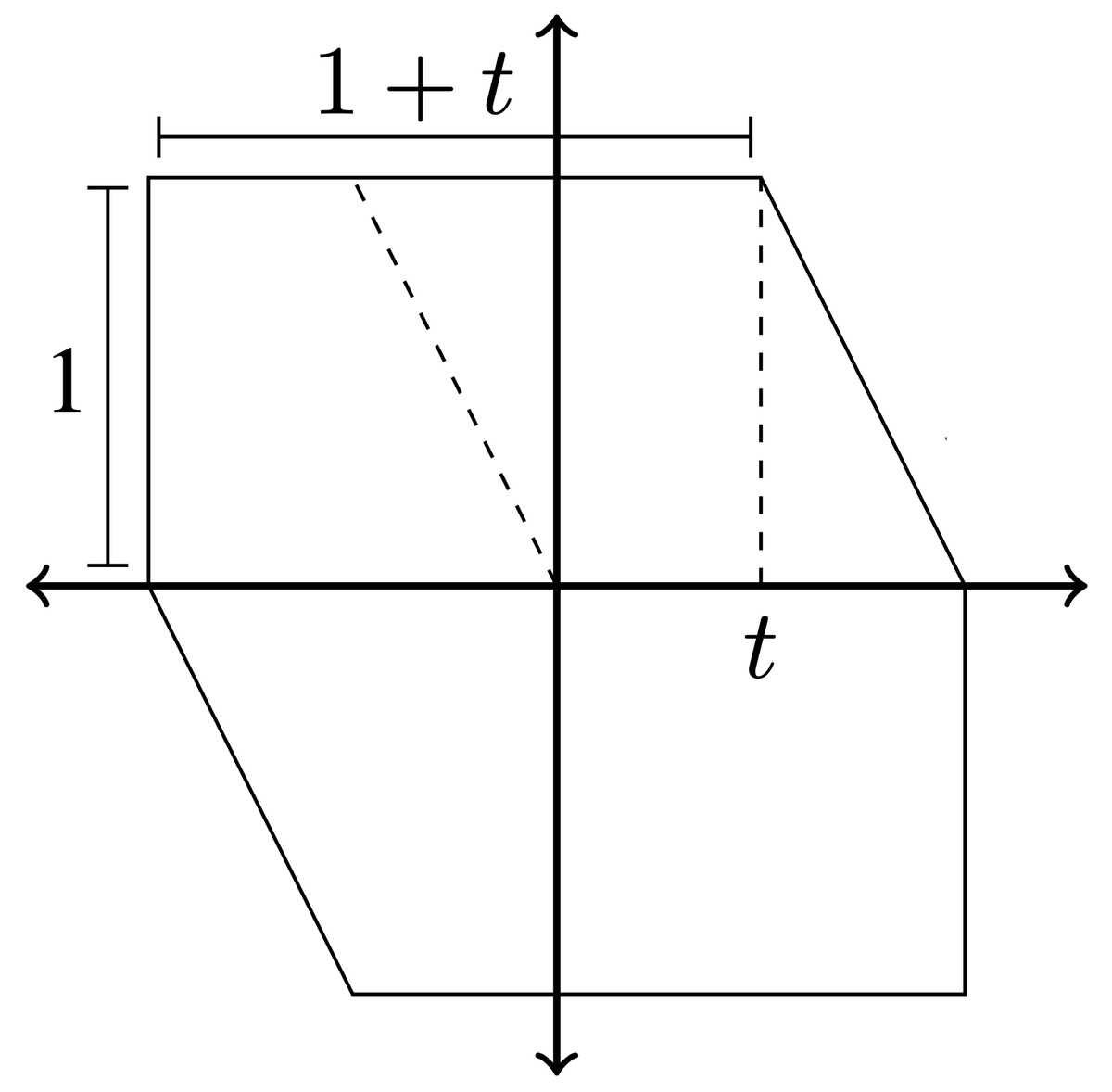
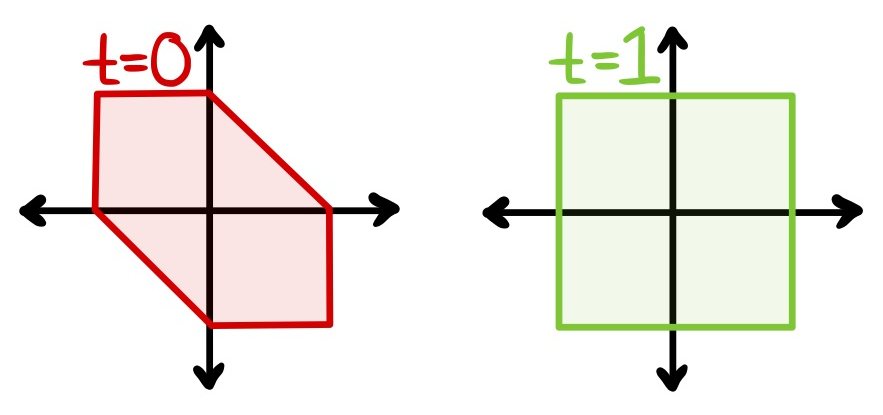
Fix some 0≤t≤1 and let B be the hexagon with vertices (±1,0), (±1,∓1), and (±t,±1) shown below. This has all the required properties to define a norm d. The length of a segment is just the distance between its endpoints, so we need only measure six different distances. (17/32)
Since (1,0) and (0,1) are both on the unit circle ∂B, vertical/horizontal distances match our usual notion. Hence, the vertical sides have total length 2 and the horizontal sides have total length 2+2t. The sloped side from (1,0) to (t,1), has length
ᵈ||(t-1,1)||. (18/32)
ᵈ||(t-1,1)||. (18/32)
But the point (t-1,1) lies on the unit circle ∂B, so
ᵈ||(t-1,1)||=1. Hence, the two sloped sides have total length 2. In all, we see that
ϖ(d)=(2+2+2t+2)/2=3+t. As t ranges from 0 to 1, we see that our "generalized pi" can achieve any value in the interval [3,4]. (19/32)
ᵈ||(t-1,1)||=1. Hence, the two sloped sides have total length 2. In all, we see that
ϖ(d)=(2+2+2t+2)/2=3+t. As t ranges from 0 to 1, we see that our "generalized pi" can achieve any value in the interval [3,4]. (19/32)
Also note that: when t=1, B is a square and ϖ(d)=4; when t=0, B is a hexagon (regular after a change of coordinates) and ϖ(d)=3. We will (cursorily) see later that these extreme values must look like this. For now, the next step is to see why 3≤ϖ(d)≤4 for any norm d. (20/32)
First, a technical lemma. For two (compact) convex regions A ⊂ B and a norm d, we have lenᵈ(∂A)≤lenᵈ(∂B). The proof, which cleverly uses the triangle inequality, can be found as Lemma 1(a) in [1]. We will take this fact for granted, so that we can move forward. (21/32)
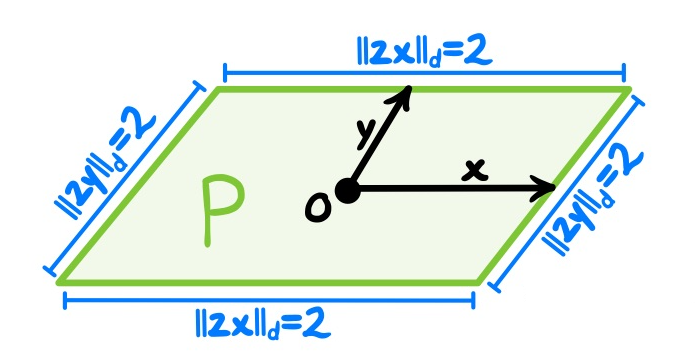
To prove that ϖ(d)≤4, we need to find a circumscribed parallelogram about Bᵈ. Specifically, we find two points x,y∈∂Bᵈ, such that Bᵈ is entirely contained in the parallelogram P={sx+ty:-1≤s,t≤1}. (Again, I don't include the proof here, but it can be found in [1].) (22/32)
The sides of P are (up to sign) the vectors 2x & 2y (each occurring twice). But x & y both lie on the unit circle ∂Bᵈ, so
lenᵈ(P)=2*ᵈ||2x||+2*ᵈ||2y||=8.
Since P is convex, we have
2ϖ(d)=lenᵈ(∂Bᵈ)≤lenᵈ(P)=8,
by our lemma. Dividing both sides by 2 gives ϖ(d)≤4. (23/32)
lenᵈ(P)=2*ᵈ||2x||+2*ᵈ||2y||=8.
Since P is convex, we have
2ϖ(d)=lenᵈ(∂Bᵈ)≤lenᵈ(P)=8,
by our lemma. Dividing both sides by 2 gives ϖ(d)≤4. (23/32)
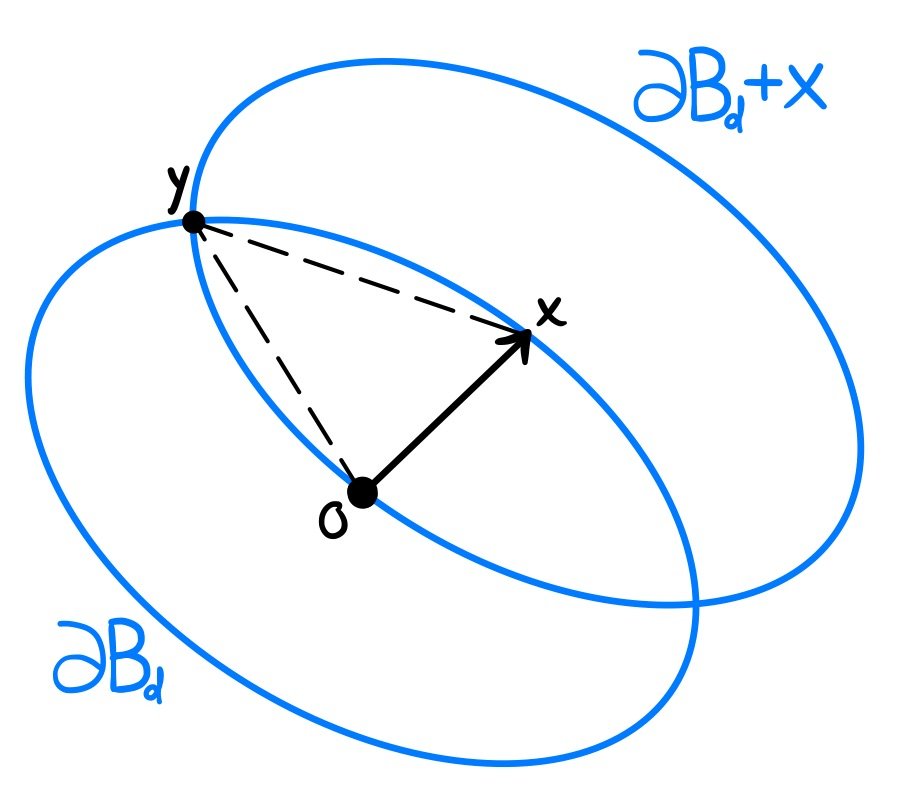
To prove that ϖ(d)≥3, we find an inscribed hexagon, similarly to the classic straightedge-compass construction of an equilateral triangle. Pick any vector x∈∂Bᵈ. The unit circle ∂Bᵈ and its translate ∂Bᵈ+x intersect in ≥2 points. Pick 1 such point and call it y. (24/32)
Since y∈∂Bᵈ+x, we have y-x∈∂Bᵈ. But we also have x,y∈∂Bᵈ, so it follows that
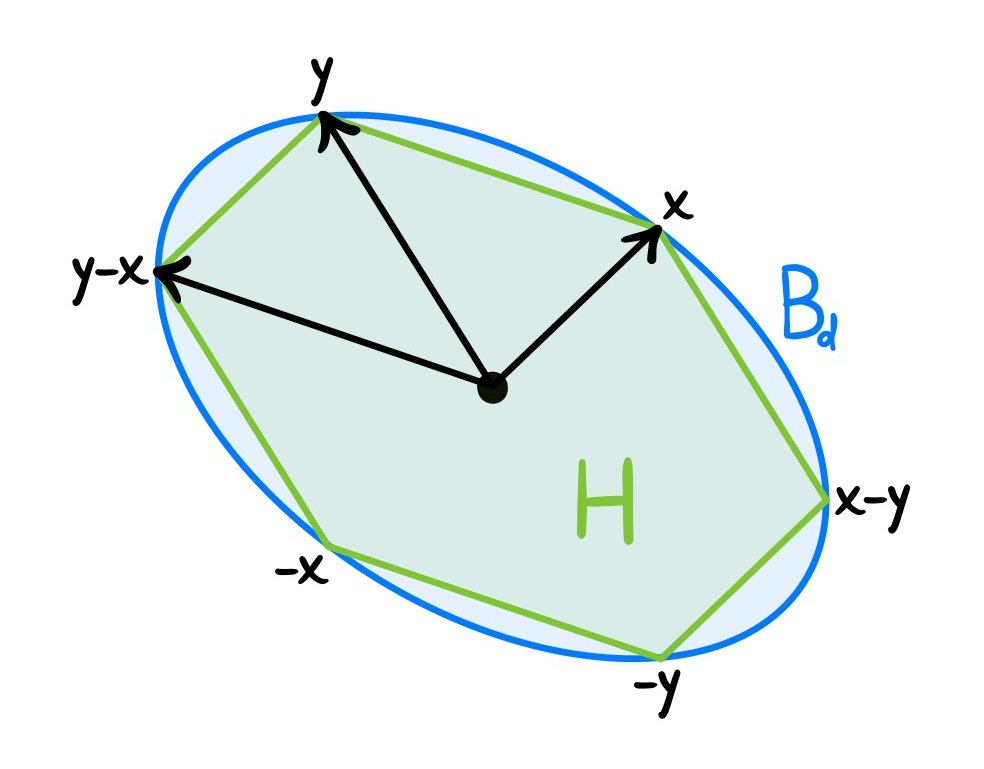
ᵈ||x||=ᵈ||y||=ᵈ||y-x||=1. Since x, y and y-x are in Bᵈ, so are their negatives -x, -y and x-y. Hence, we define the hexagon H⊂Bᵈ whose vertices are ±x, ±y, x-y and y-x. (25/32)
ᵈ||x||=ᵈ||y||=ᵈ||y-x||=1. Since x, y and y-x are in Bᵈ, so are their negatives -x, -y and x-y. Hence, we define the hexagon H⊂Bᵈ whose vertices are ±x, ±y, x-y and y-x. (25/32)
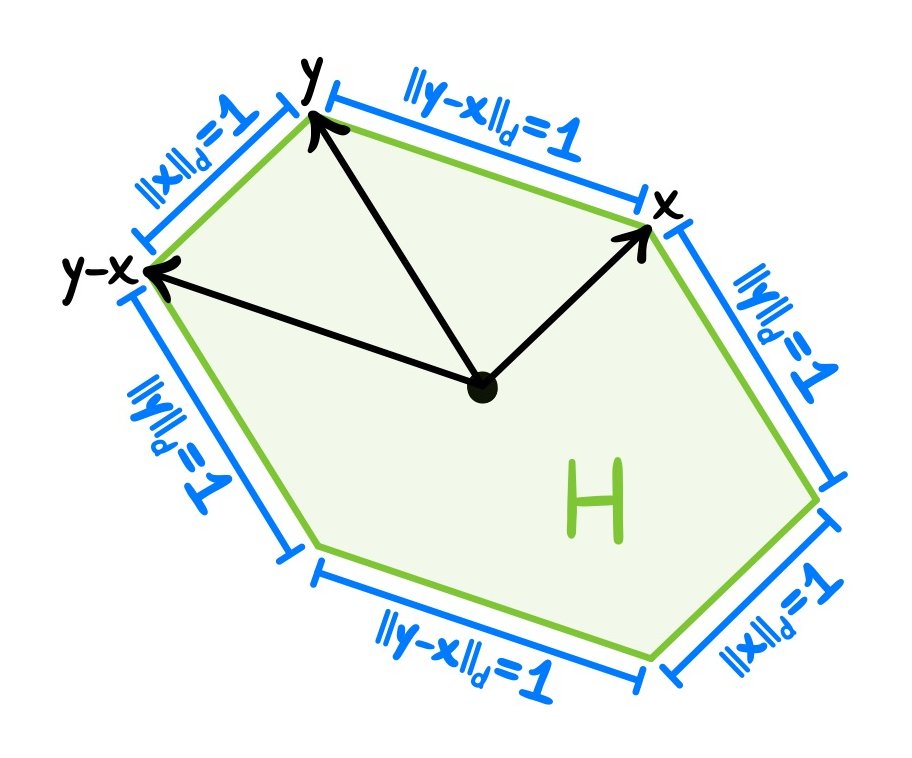
The sides of H are (up to sign) the vectors x, y and y-x (each occurring twice). Therefore
lenᵈ(H)=2*ᵈ||x||+2*ᵈ||y||+2*ᵈ||y-x||=6.
Since H is convex, we have
2ϖ(d)=lenᵈ(∂Bᵈ)≥lenᵈ(H)=6.
Dividing both sides by 2 gives ϖ(d)≥3. (26/32)
lenᵈ(H)=2*ᵈ||x||+2*ᵈ||y||+2*ᵈ||y-x||=6.
Since H is convex, we have
2ϖ(d)=lenᵈ(∂Bᵈ)≥lenᵈ(H)=6.
Dividing both sides by 2 gives ϖ(d)≥3. (26/32)
These results are due to Stanisław Gołąb, who posed and solved the problem in a paper published in 1932. He also classified the extremal cases: ϖ(d)=4 if and only if Bᵈ is a parallelogram, while ϖ(d)=3 if and only if Bᵈ is an “affine regular” hexagon. (27/32)
The proofs of the extremal cases are more technical, but they boil down to comparing Bᵈ with the circumscribed/inscribed parallelogram/hexagon and showing that strict containment leads to a strict inequality. For an accessible account of the full proofs that 3≤ϖ(d)≤4… (28/32)
… I recommend [1] “On the Values of Pi for Norms on ℝ2” by Duncan, Luecking & McGregor, printed in the 𝘊𝘰𝘭𝘭𝘦𝘨𝘦 𝘔𝘢𝘵𝘩 𝘑𝘰𝘶𝘳𝘯𝘢𝘭. Proofs of the extreme cases can be found in §4.3 of Thompson’s 𝘔𝘪𝘯𝘬𝘰𝘸𝘴𝘬𝘪 𝘎𝘦𝘰𝘮𝘦𝘵𝘳𝘺. Since the latter text … (29/32)
… might seem formidable to some readers, I set out to write an accessible account, in the style of [1], with proofs of the extreme cases. Unfortunately, my version ended up being more technical than I wanted. But [1] also has an interesting, original result: … (30/32)
… if d has quarter turn symmetry, then ϖ(d)≥π, the classical value! I did manage to prove the extreme case of that result, showing that d has quarter-turn symmetry and ϖ(d)=π if and only if Bᵈ is an ellipse (i.e. d arises from an inner product). (31/32)
That writing is currently under double-masked consideration (which I'm all for, btw), but I will post it here when I get rejected and it is appropriate to do so…
If you made it all the way down here, thank you so much for reading!!! (32/32) (and rt if you think it deserving?)
If you made it all the way down here, thank you so much for reading!!! (32/32) (and rt if you think it deserving?)

 Read on Twitter
Read on Twitter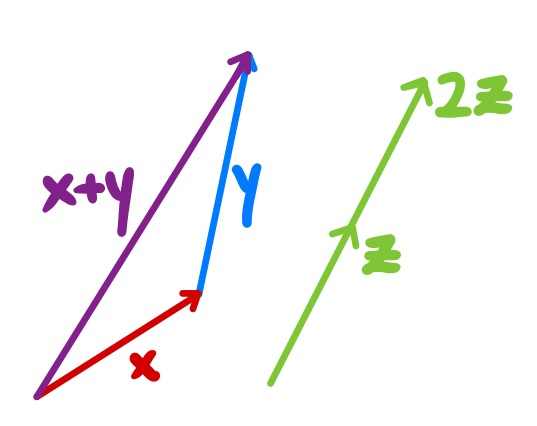
![Partitioning a path γ:[0,1]→ℝ² into finitely many steps 0=t₀≤t₁≤…≤tᵢ=1 affords us an "estimation” of its length:d(γ(t₀),γ(t₁))+d(γ(t₁),γ(t₂))+…+d(γ(tᵢ₋₁),γ(tᵢ)).But these points may miss some of the path’s curviness, giving too small a value. (11/32) Partitioning a path γ:[0,1]→ℝ² into finitely many steps 0=t₀≤t₁≤…≤tᵢ=1 affords us an "estimation” of its length:d(γ(t₀),γ(t₁))+d(γ(t₁),γ(t₂))+…+d(γ(tᵢ₋₁),γ(tᵢ)).But these points may miss some of the path’s curviness, giving too small a value. (11/32)](https://pbs.twimg.com/media/Eq6ObvAVkAAcDVQ.png)
![But the point (t-1,1) lies on the unit circle ∂B, so ᵈ||(t-1,1)||=1. Hence, the two sloped sides have total length 2. In all, we see that ϖ(d)=(2+2+2t+2)/2=3+t. As t ranges from 0 to 1, we see that our "generalized pi" can achieve any value in the interval [3,4]. (19/32) But the point (t-1,1) lies on the unit circle ∂B, so ᵈ||(t-1,1)||=1. Hence, the two sloped sides have total length 2. In all, we see that ϖ(d)=(2+2+2t+2)/2=3+t. As t ranges from 0 to 1, we see that our "generalized pi" can achieve any value in the interval [3,4]. (19/32)](https://pbs.twimg.com/media/Eq6S4-4UcAAR-Qs.png)
![First, a technical lemma. For two (compact) convex regions A ⊂ B and a norm d, we have lenᵈ(∂A)≤lenᵈ(∂B). The proof, which cleverly uses the triangle inequality, can be found as Lemma 1(a) in [1]. We will take this fact for granted, so that we can move forward. (21/32) First, a technical lemma. For two (compact) convex regions A ⊂ B and a norm d, we have lenᵈ(∂A)≤lenᵈ(∂B). The proof, which cleverly uses the triangle inequality, can be found as Lemma 1(a) in [1]. We will take this fact for granted, so that we can move forward. (21/32)](https://pbs.twimg.com/media/Eq6Ts4eUYAE9zEd.png)
![To prove that ϖ(d)≤4, we need to find a circumscribed parallelogram about Bᵈ. Specifically, we find two points x,y∈∂Bᵈ, such that Bᵈ is entirely contained in the parallelogram P={sx+ty:-1≤s,t≤1}. (Again, I don't include the proof here, but it can be found in [1].) (22/32) To prove that ϖ(d)≤4, we need to find a circumscribed parallelogram about Bᵈ. Specifically, we find two points x,y∈∂Bᵈ, such that Bᵈ is entirely contained in the parallelogram P={sx+ty:-1≤s,t≤1}. (Again, I don't include the proof here, but it can be found in [1].) (22/32)](https://pbs.twimg.com/media/Eq6UQHqVgAEbgYS.png)