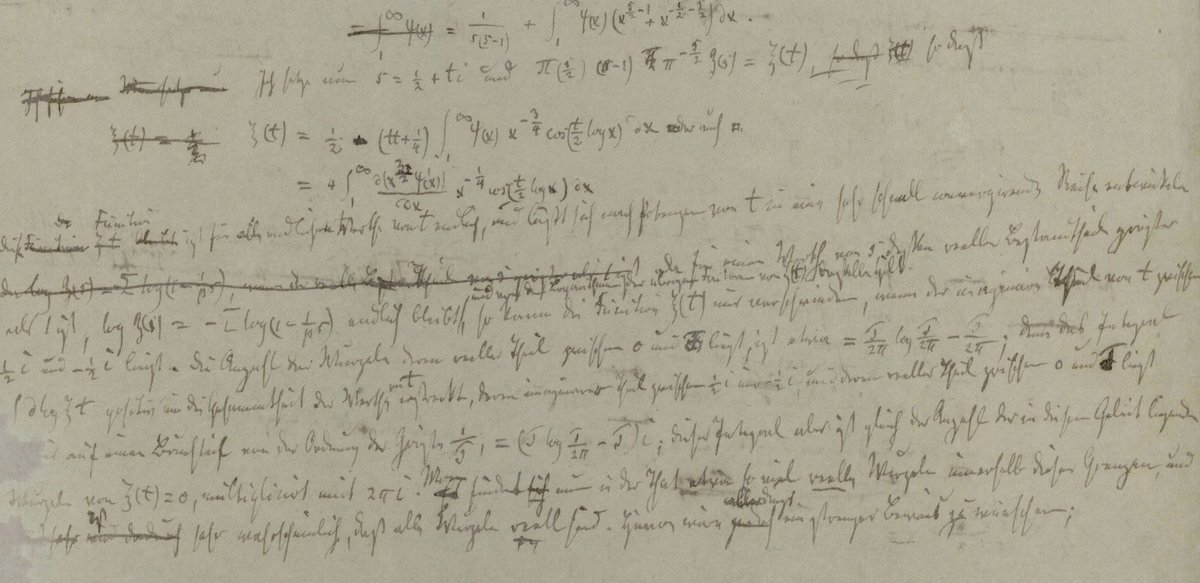Well known number theorists : conjectures f(x) < 1 for all x

Pair of well known number theorists : proves limsup f(x) > 1.06 and conjecture that f(x) is unbounded.

If that ain't faith…

To be serious, the previous thread is prompted bya rapid browse at a paper of Odlyzko and te Riele where they disprove a conjecture of Mertens related to the Riemann zeta function.

And to deserve your forgiveness after this hint of sarcasm, here's the actual story. (A thread)

This is related to prime numbers, those integers (larger than 1) which are only divisible by 1 or themselves: 2, 3, 5, 7, 11, 13, etc., Etc., because, since Euclid, we know that there are infinitely many of them.

Mathematicians have been naturally attracted by them, in particular, they wish to understand how much prime numbers there are below any given bound. They could have wished for a formula enumerating the primes, but they don't smoke enough stuff for that.

The Prime number theorem, proved by Hadamard and de la Vallée Poussin at the beginning of the 20th century, says that there are roughly x/log(x) prime numbers below a bound x, when x grows to infinity. But to have a less rough understanding of this behaviour is a daunting task.

In 1859, Riemann had introduced a function of a complex variable (the Riemann zeta function) and made the hypothesis that the only zeroes of this function are of the form 1/2 + i (something), understanding how this would govern the behavious of the primes.

(Actually, there are other zeroes, at the even negative integers, but we understand them so well that they are considered as “trivial zeroes”.)

Now comes Franz Mertens… He had shown an early result towards the Prime number theorem, estimating how the series of the inverses of the primes (1/2 + 1/3 + 1/5 + 1/7 + …) diverges to infinity when you sum more and more terms…

In fact, Euler had already shown that result, as well as Legendre, and Tchebychev. But all explanations of this result were at most convincing, but insufficient to be considered as an actual proof.

By the way, here is Actual Proof.
Herbie Hancock on piano, Vinnnie Colaiuta on drums, Talk Wilkenfeld on bass.

There's something bizarre with the Riemann hypothesis, that it involves complicated quantities, and mathematicians have got attracted with more elementary looking formulations.

One of them involves the Möbius function: for any integer n, µ(n) is 0 if n is divisible by the square of a prime, and otherwise, it is 1 if n is divisible by an even number of prime numbers, and -1 if n is divisible by an odd number of prime numbers.

This function takes only three different values, 0, 1 and -1, but its behavior looks erratic : its first values are 1, -1 , -1, 0, -1, 1, -1, 0, 0, 1, -1, 0, -1, 1, 1…
It seems somebody chose those numbers randomly…

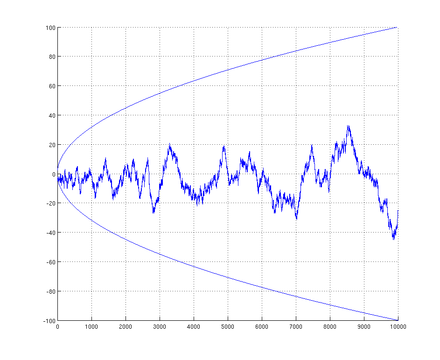
To get a better understanding, one can look at their values on average : sum all µ-values up to a bound x, and look at the behavior of the resulting sum M(x).
This is usually very efficient, for it smoothes down all these tiny variations.

If you do this with randomly chosen ±1, you'd get a function growing roughly like the square root of x.
And Mertens conjectured that | M(x) | < √x for all x.
(Picture, Wikipedia, M(x) for x less than 10 000.)

As a matter of fact, if you could prove that, or even that M(x)/ √x remains bounded, then you'd obtain a proof of the Riemann hypothesis. (See the Wikipedia webpage if you don't believe me, or do the proof…)
https://en.wikipedia.org/wiki/Mertens_conjecture

This was a very old conjecture, for Stieltjes had already claimed in 1885 that M(x)/√x remains bounded, and Mertens refined it as | M(x) | < √x, based on explicit computations for x up to 10000.

However, one century later, Odlyzko and te Riele proved that this conjecture was false : they proved that there are values of x with M(x) > 1.06 √x,
values of x with M(x) < -1.009 √x.
http://www.dtc.umn.edu/~odlyzko/doc/arch/mertens.disproof.pdf

But, this may sound astonishing to any non-mathematician which had not flew away at the vision of all these white bald-or-bearded mathematiciens, they did not produce any value of x such that M(x) > √x, nor any value of x with M(x) < - √x. They just proved that some exist…

They say they suspect that there are no such x smaller than 10^30 (1 followed by 30 zeroes…).

They also say that they suspect, in fact, that M(x)/√x is unbounded, and they believe so because of the random model about the Möbius function: if µ(n) were random, one would expect a √x-like growth, but with spikes of the form √(x log(log(x)).

What led Odlyzko and te Riele to prove this result (besides being excellent analytic number theorists, I mean), is that they could estimate various quantities in terms of the imaginary parts of non-trivial zeroes of the Riemann zeta function,

and the presumption that hey would not satisfy any linear relation with integral coefficients. Just because there is no reason for. This principle had already been put forward by Ingham, in the direction of a disproof of the Mertens conjecture.

But, as they say, recent work in Diophantine approximation, notably the Lenstra-Lenstra-Lóvasz algorithm allowed them to exhibit the large enough linear combinations required by the idea of a disproof.

I have to stop here, because Twitter does not let me add any more tweet. So here is the initial tweet that prompted my curiosity and this short story. https://twitter.com/MathAndCobb/status/1344028472205860871?s=20