There is a lot of often overlooked evidence that standard p(w) = N(0, a*I) priors combined with a NN f(x,w) induce a distribution over functions p(f(x)) with useful properties!... 1/15
The deep image prior shows this p(f(x)) captures low-level image statistics useful for image denoising, super-resolution, and inpainting. The rethinking generalization paper shows pre-processing data with a randomly initialized CNN can dramatically boost performance. 2/15
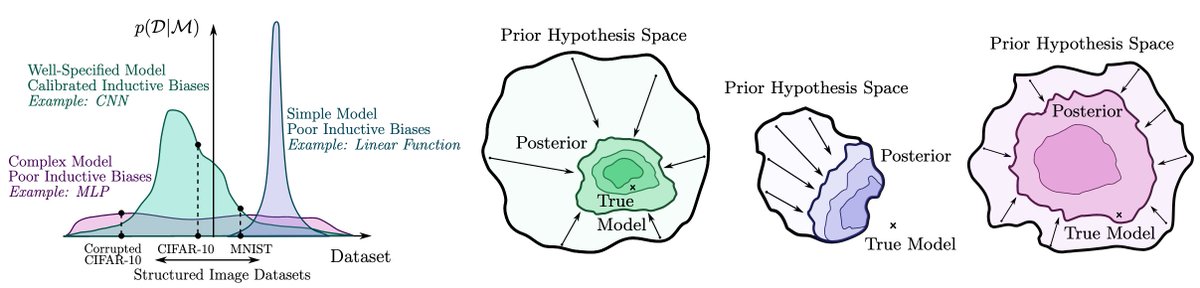
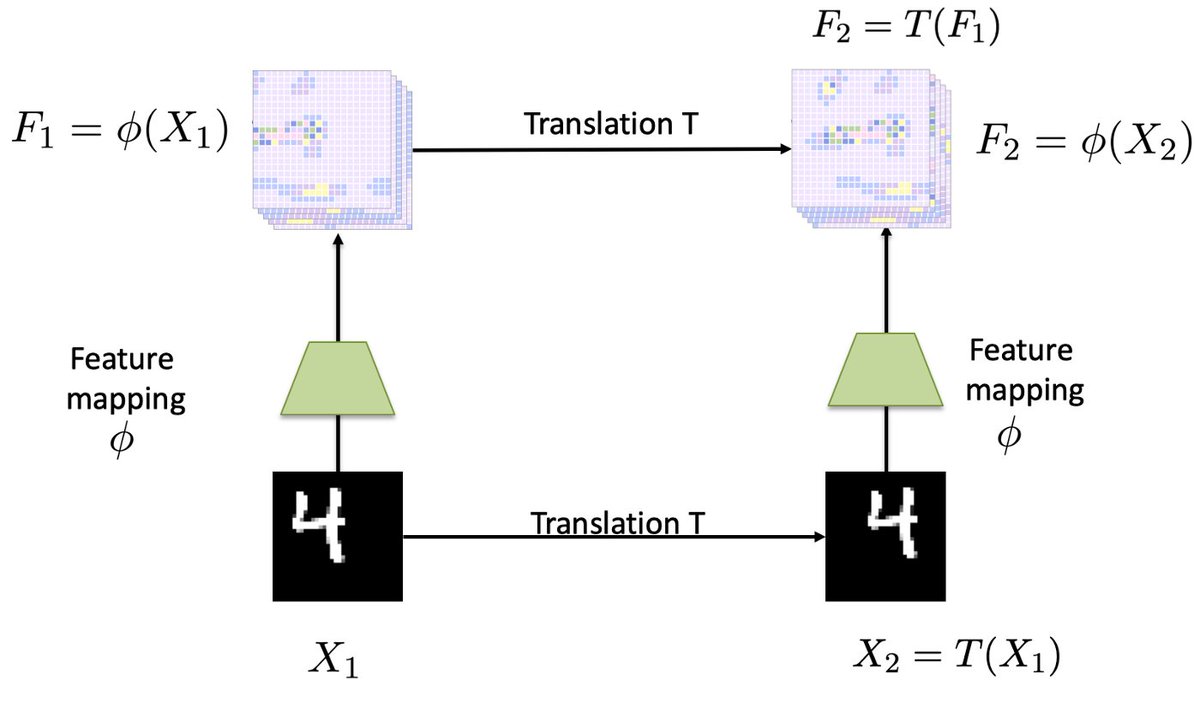
We show that the induced p(f(x)) has a reasonable correlation function, such that visually similar images are more correlated a priori. Moreover, the flatness arguments for SGD generalization suggest that good solutions take up a large volume in the corresponding posteriors. 3/15
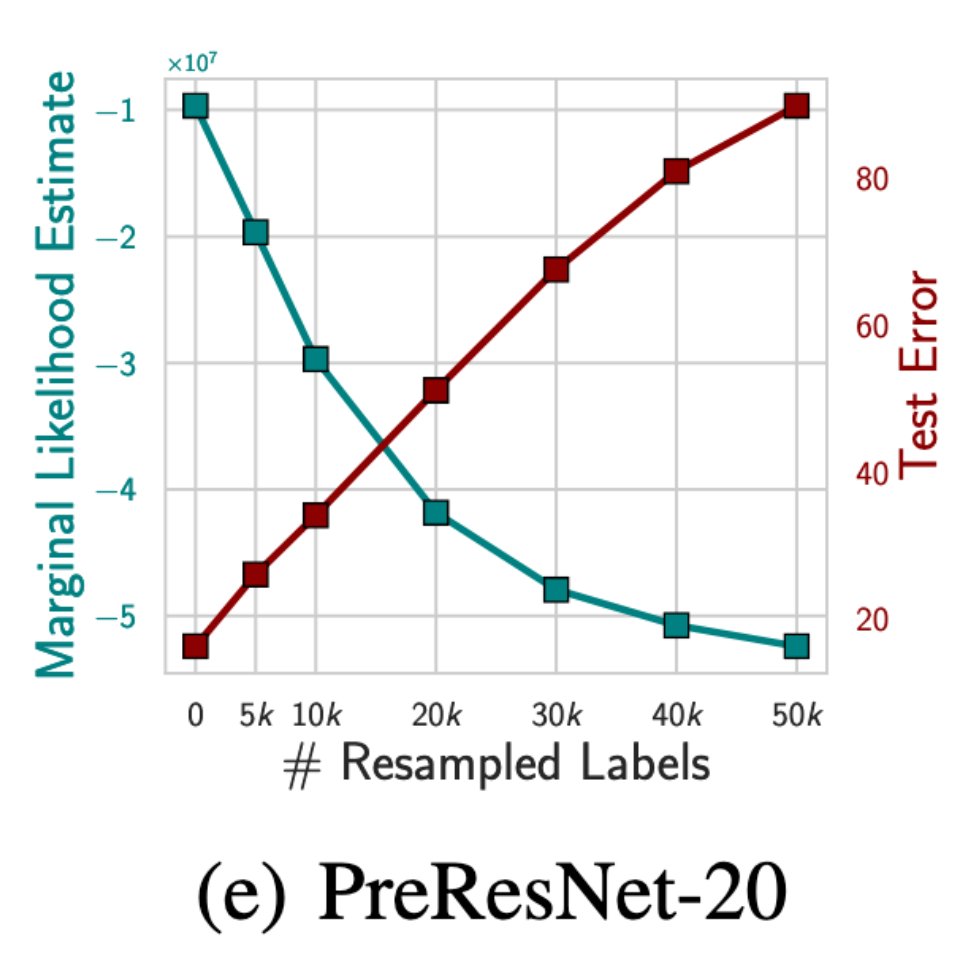
We can also quantify this intuition and show that this prior leads to a marginal likelihood that favours structured image datasets over noisy image datasets, even if the network is able to perfectly fit the noisy datasets. 4/15
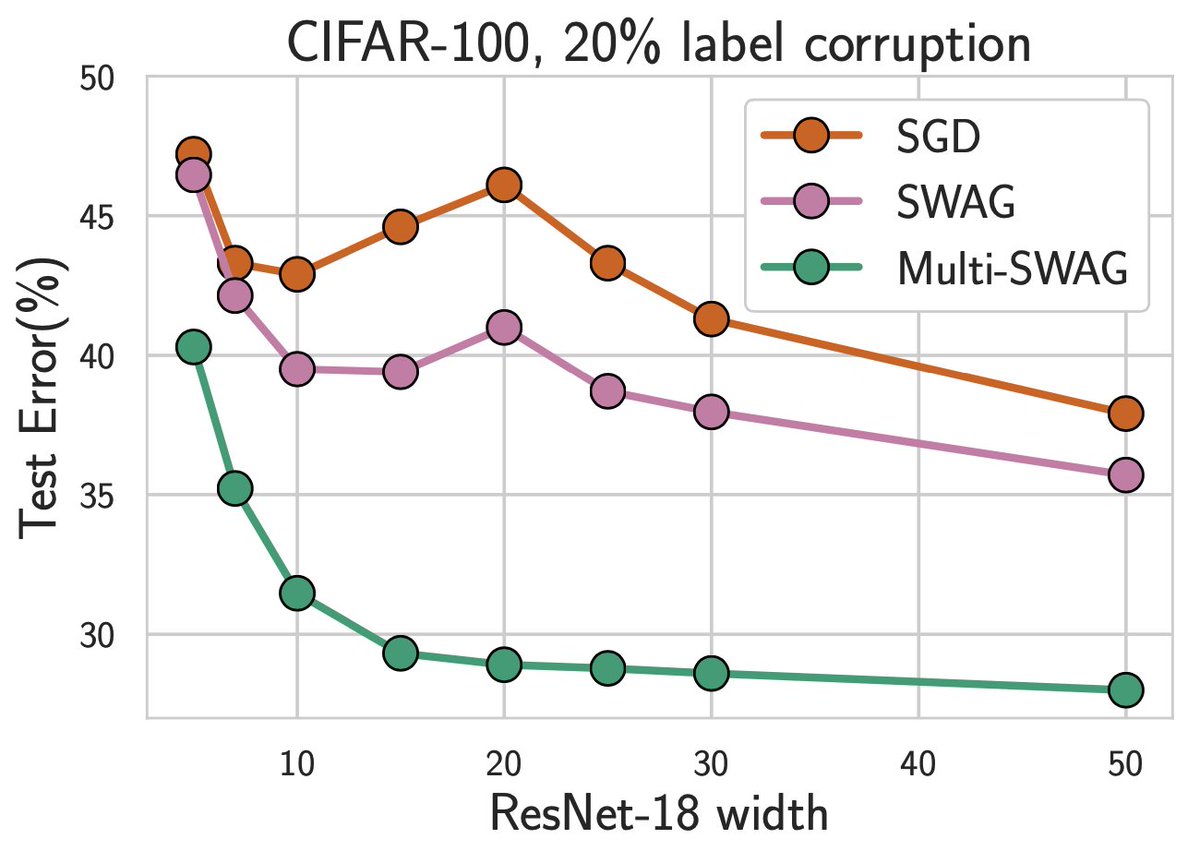
We also show these priors lead to posteriors that can alleviate double descent and provide significant performance gains! There are indeed *many* results showing BMA improves performance. Part of the skepticism about priors stems from the misconception that BDL doesn't work. 5/15
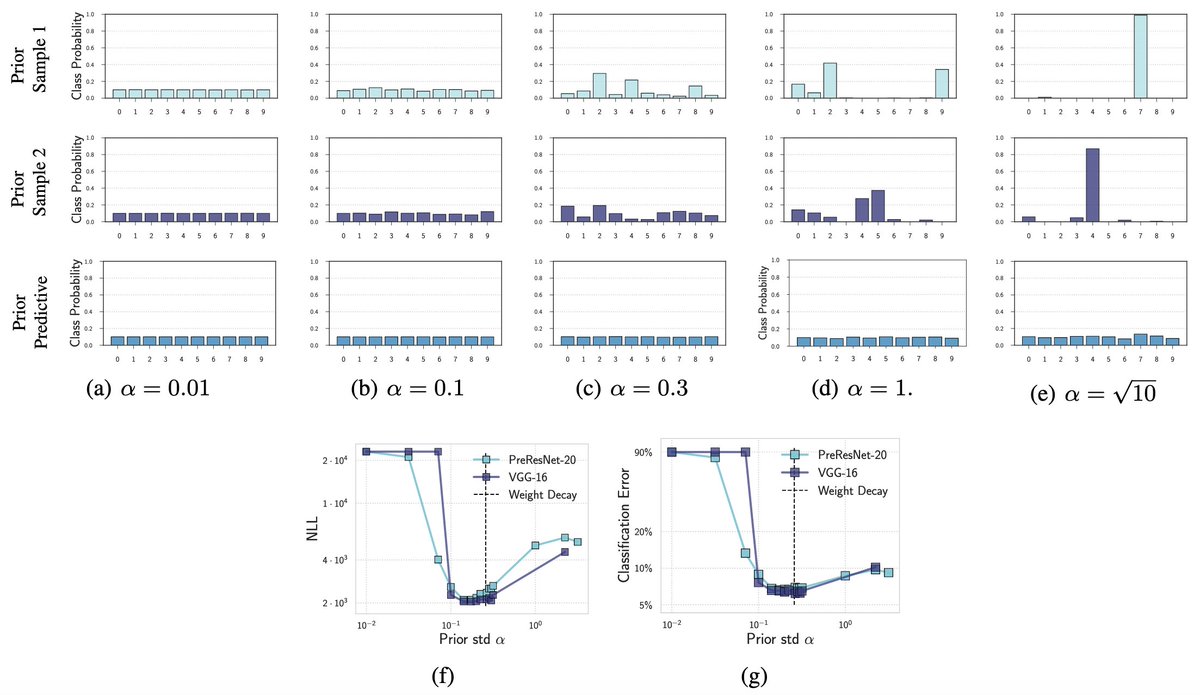
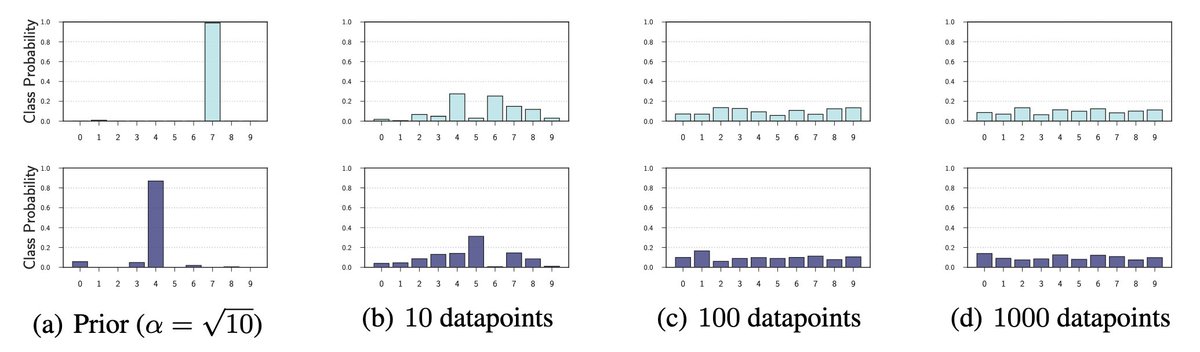
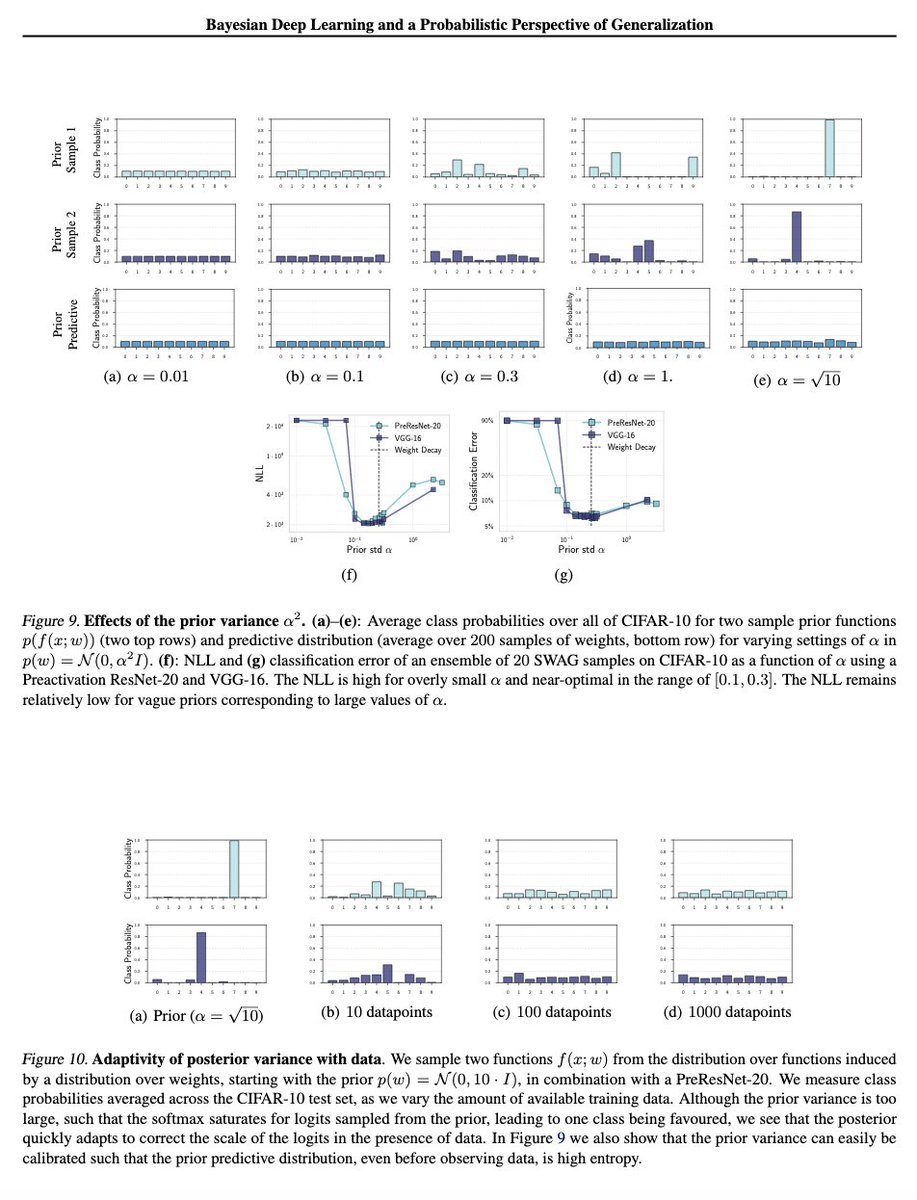
What about the result showing that samples from p(f(x)) assign nearly all data to one class? We show that is an artifact of choosing a bad signal variance 'a' in the N(0,a*I) prior, such that the softmax saturates. The 'a' is easy to tune, correcting this behaviour. 6/15
This is also a very soft prior bias, which is quickly modulated by data. Even after observing a little data, we see the bias quickly goes away in the posterior. We also see the actual predictive distribution (prev plot, row 3), even in the misspecified prior, is reasonable! 7/15
These nice results are intuitive. Many of the function-space properties of the prior, such as translation equivariance, are controlled by the architecture design. Designing a better prior would largely amount to architecture engineering. 8/15
But what about cold posteriors? Is it troubling that we sometimes improve results with T<1? While interesting, this is not necessarily bad news for BDL. There are many reasons this can happen, even with a well-specified prior and likelihood, Sec 8 ( https://arxiv.org/pdf/2002.08791.pdf). 9/15
Can the priors be improved? Certainly. Architecture design would be a key avenue for improvement. In some cases, I am puzzled by choosing a p(w) that induces a p(f(x)) that is like a GP with a standard kernel. Are we throwing the baby out with the bathwater? 10/15
Why do this? Don't we already have GPs with standard kernels? NNs are a distinct model class precisely because they have useful complementary inductive biases. While the standard p(f(x)) from p(w)=N(0,a*I) may be hard to interpret, that doesn't make it bad. 11/15
A reason for GP-like priors could be an asymptotic computational advantage over regular GPs. But we have many methods directly addressing GP scalability. Maybe a closed form expression for posterior samples? But this is not how they are often motivated. 12/15
Sometimes Masegosa's nice work ( https://arxiv.org/abs/1912.08335 ) is used by others to claim we need better weight space priors. But misspecification in that paper is about not having enough support! Changing p(w) from N(0,a*I) is not going to help enlarge prior support! 13/15
I'm supportive of work trying to improve weight-space priors. But let's be careful not to uncritically adopt an overly pessimistic narrative because it appears "sober" and is a convenient rationalization for paper writing. Something doesn't need to be bad to make it better. 14/15
In short, there are many reasons to be optimistic! @Pavel_Izmailov and I discuss these reasons, and many other points, in our paper "Bayesian Deep Learning and a Probabilistic Perspective of Generalization": https://arxiv.org/abs/2002.08791 . 15/15

 Read on Twitter
Read on Twitter