Morse theory thread! Unfortunately not as general as I'd like it to be, but if you skim over some bits it should be interesting enough even if you've only a rough idea what a manifold and function is
1/21
1/21
So maths largely is analysis, geometry, and algebra. Morse theory says analysis and geometry should be done together. Analysis is the largely the study of functions, and geometry is the study of shapes. Shapes for us means smooth manifolds, and functions are smooth real valued
2/
2/
We want to study manifolds by looking at the possible functions on it, so what's the goal? We'd like a way to reconstruct a manifold given a function on it. Turns out this is actually very doable. Let's look at the classical example-
3/21
3/21
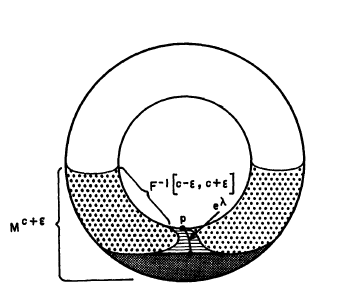
Place a torus upright with it's base touching the origin of R^3 and consider the function f given by its height above the xy-plane. Then we can look at how the level sets of f change as we move up in height
4/21
4/21
We look at the "prelevel sets": draw a line at a given height and consider the shape below that line. We can think of this as slowly filling space with water- we're interested in what's below the water at a given time
5/21
5/21
Looking at the picture we see that the homotopy type of the prelevel sets only changes at certain points, i.e. the shape looks mostly the same, just stretched a bit until we pass certain points, then it permanently changes.
6/21
6/21
So now we ask: what points cause the homotopy type to change, and can we tell how it will change based on the function at that point? The first answer is that these are the critical points of f ! The second answer is more involved, but here's a teaser for later:
7/21
7/21
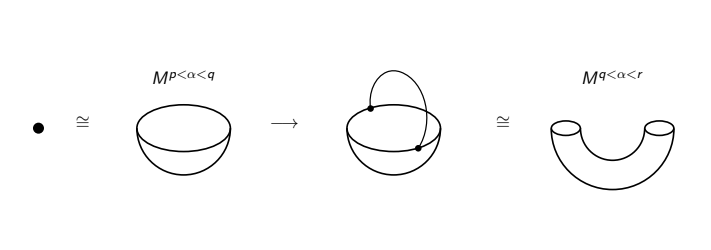
Now, how does the function at a critical point determine the manifold's shape? Claim: passing a critical point with k linearly independent decreasing directions causes a k-cell to be added to the prelevel set. This will take some work
8/21
8/21
First, what's a k-cell? This is worth its own thread but:
-A 0-cell is a point
-A 1-cell is a line segment
-A 2-cell is a disk
etc.
They're pretty much k-dimensional building blocks for a topological space.
9/21
-A 0-cell is a point
-A 1-cell is a line segment
-A 2-cell is a disk
etc.
They're pretty much k-dimensional building blocks for a topological space.
9/21
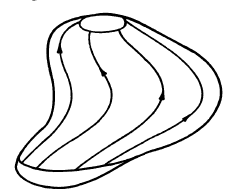
Now, why does the homotopy type not change away from critical points? A way to see this is to consider the gradient of the function - This is non-zero away from crits, so the gradient flow lines actually provide a diffeomorphism between the prelevel sets! (pic from Milnor)
10/21
10/21
Now what happens at a critical point? This one is a bit harder to prove. First we need the Morse lemma: around any non-degenerate critical point of a function there are coordinates such that f is a sum of ± squares of the coordinates
11/21
11/21
(nerd tweet): We prove this by diagonalising the Hessian, using the inverse function theorem to show what we get is a smooth chart. The number of negative signs is the number of decreasing directions, called the index of the critical point.
12/21
12/21
Finally to prove that passing a critical point of index k corresponds to attaching a k-cell we use the previous two results along with some clever choices of functions and playing with retracts. Details in Milnor, I'm more interested in using the results.
13/21
13/21
Going back to the diagram earlier you should now be able to see how it works: at the origin there are 0 decreasing directions, so add a 0-cell, which is homeo to a 2-cell in R^3. Passing the hole opening there is one decreasing dirn, so add a 1-cell. deform to a cylinder
14/21
14/21
At the top of the hole there is again one decreasing dirn, so add another 1-cell and deform to get a torus with a disk removed, finally at the top we have two decreasing directions, so add a 2-cell to give the whole torus! So we've built the torus from its height!
15/21
15/21
Here's an application: The Reeb Sphere Theorem - If a compact manifold has a function on it with exactly
two non-degenerate critical points it's homeomorphic to a sphere.
16/ 21
two non-degenerate critical points it's homeomorphic to a sphere.
16/ 21
At the base we add a 0-cell (homeo to an n-cell), at the top we add an n-cell, no crits in between means each pre-level set is a deformation retract of the others, so the two n-cells must be attached normally along their boundary, hence we have a sphere!
17/21
17/21
Fun fact: This was how Milnor showed his exotic 7-sphere was topologically a sphere. It's a really useful test. There are lots of similar results to this.
18/21
18/21
I should probably talk about some of the assumptions here: I ignored the compact requirement for convenience, but what about degenerate critical points? It's actually a consequence of Sard's theorem that functions w no non-degen crits are dense in the set of smooth real fns
19/21
19/21
I'll end with some teasers about where things go next:
-Using these theorems we can construct a homology theory - Morse homology
-We can move all this to variational calculus: decreasing directions correspond to geodesics etc.
20/21
-Using these theorems we can construct a homology theory - Morse homology
-We can move all this to variational calculus: decreasing directions correspond to geodesics etc.
20/21
Once again if this was fun or useful and you have money to spare, consider tipping me?
(please don't give money if you're struggling!!):
https://ko-fi.com/elhayes
Also please let me know if there's anything else I can do for accessibility
21/21
(please don't give money if you're struggling!!):
https://ko-fi.com/elhayes
Also please let me know if there's anything else I can do for accessibility
21/21
I'm not happy with this, it could definitely be made more accessible, but it resists the tweet format. Here's the slides of a more formal talk I gave on this:
https://drive.google.com/file/d/1oZSCAa9hOMZxoiuQHrsUufunC04NjhrT/view?usp=sharing
https://drive.google.com/file/d/1oZSCAa9hOMZxoiuQHrsUufunC04NjhrT/view?usp=sharing

 Read on Twitter
Read on Twitter