The Rees ring R[It] is isomorphic as a graded ring to R
\\oplus I \\oplus I² \\oplus I³ \\oplus ... etc.,
i.e., the direct sum of the powers of I,where the degree d piece is represented by the d-th power of the ideal I.

(35/48)

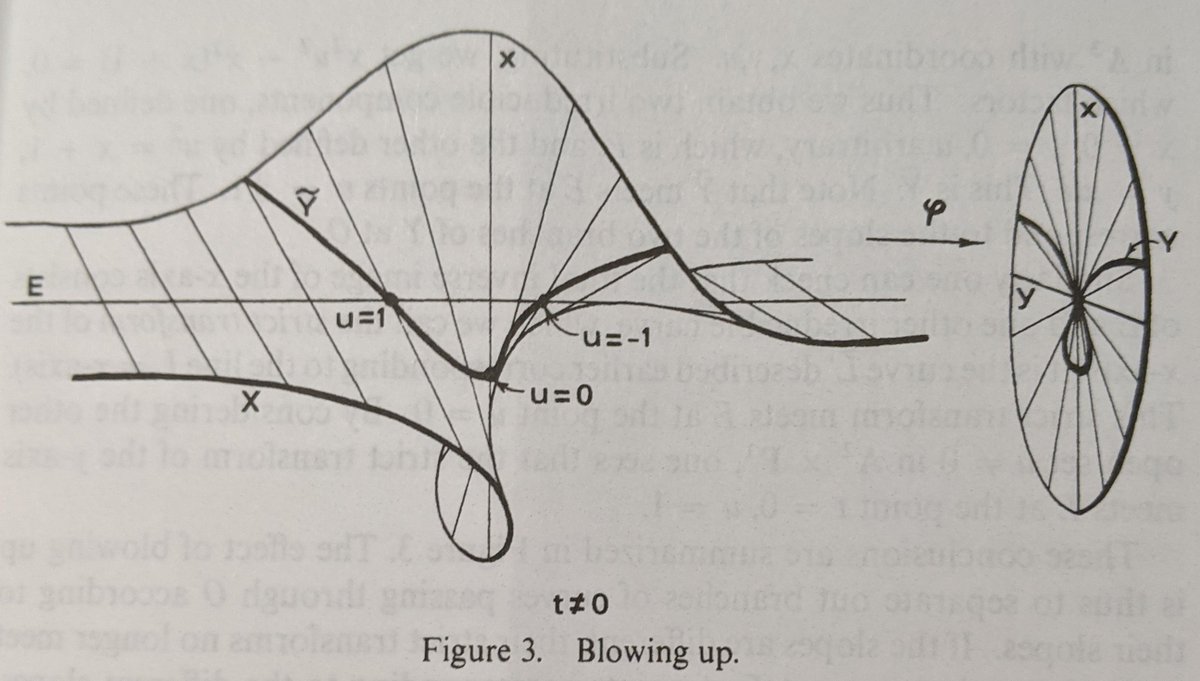
One thing we care about is the exceptional fiber of the blowup. These are the points of the blowup that project onto the subshape along which we are blowing up. In the classic blowup picture, the exceptional fiber is given by the curve E.

(36/48)

To find the homogeneous coordinate ring of the exceptional fiber, we can again think about restricting our functions to just the exceptional set. Note that the exceptional set projects onto the points defined by our ideal I.

(37/48)

This means that the generators of the ideal I vanish on the subshape along which we are blowing up. Said another way, the generators of I are indistinguishable from the 0 function on the exceptional set.

(38/48)

Thus, we see that the homogeneous coordinate ring of the exceptional set should be the homogeneous coordinate ring of the blowup modulo the extension of I. In other words, R[It]/IR[It]. This ring is called the associated graded ring of I, and is sometimes denoted G(I).

(39/48)

The associated graded ring G(I) is isomorphic as a graded ring to
R/I \\oplus I/I² \\oplus I²/I³ \\oplus I³/I⁴ \\oplus ... etc.,
where the degree d piece is represented by the d-th power of the ideal I modulo the (d+1)st power of the ideal I.

(40/48)

Another part of the blowup one might care about is the special fiber. If the origin lives inside the shape you're blowing up, then you might care about what part of the blowup projects onto the origin. This is the special fiber of the blowup.

(41/48)

(Note: in our particular example of blowing up the curve given by y²-x³-x² = 0 at the origin, the special fiber is the same thing as the exceptional fiber. However, in general, you may not be blowing up along a subshape containing the origin.)

(42/48)

So what's the homogeneous coordinate ring of the special fiber? Well, we note that if we restrict to the special fiber, then the ideal corresponding to the origin is indistinguishable from the 0 function.

(43/48)

So let m denote the ideal corresponding to the origin (for example, if you're in F[x,y,z], the origin corresponds to m = (x,y,z), since the vanishing of all three coordinates is the origin).

(44/48)

Then the homogeneous coordinate ring of the special fiber is given by the ring R[It]/mR[It]. This is often denoted by F(I) and is called the "special fiber ring of I".

(45/48)

So we see that there are three important rings associated with blowups, the Rees ring R[It] (sometimes denoted R(I)), the associated graded ring G(I), and the special fiber ring F(I). These are the blowup algebras.

(46/48)

These blowup algebras are of great importance in a number of areas in algebraic geometry and commutative algebra, not just limited to the context of blowups.

In the future, I plan to showcase how these blowup algebras arise in other contexts as well.

(47/48)

So thank you for reading my very long thread! I hope it was understandable and interesting!

If I have made any mistakes (which I would be shocked if I hadn't), feel free to correct me!

(48/48)

EXERCISE: In the classical picture of a blowup from Hartshorne, we get a kind of "twisted" surface that the blowup lives on. This represents the blowup of the real plane at the origin. Convince yourself that the blowup of the plane at the origin is a (noncompact) Möbius band.