A thread on blowup algebras! The blowup perspective!

(In this thread, I denote the field of real numbers as "RR".)

(1/48)

Let's begin with the basics of algebraic geometry. How can you study a geometric shape which is cut out by polynomials? Let's say, for example, that you're looking at the unit circle centered at the origin in the real plane RR².

(2/48)

We're familiar with the idea of describing this circle algebraically. Points in RR² can be represented as ordered pairs (a,b). And the circle can be described as the set of all points (a,b) satisfying a²+b² = 1.

(3/48)

For any algebraic [insert subject here], we use the tools of algebra to study [insert subject here]. For geometry, we can study the collection of polynomial functions defined on our shape. Note that I said polynomial *functions* and not polynomials.

(4/48)

If we look at RR² itself, these polynomial functions should be able to take in two inputs. Indeed, any polynomial in two variables is a unique polynomial function defined on RR². The collection of these polynomial functions forms a ring.

(5/48)

The ring of polynomial functions defined on a shape is called the coordinate ring. The coordinate ring for RR² is RR[x,y], the ring of polynomials in x and y with coefficients in RR.

(6/48)

So what's the coordinate ring for the unit circle? It makes sense to restrict the polynomial functions from RR² to this circle. But notice something interesting here! The function x²+y²-1 is indistinguishable from the 0 function when restricted to the circle!

(7/48)

In general, any polynomial in the ideal generated by x²+y²-1 is indistinguishable from the 0 function when restricted to the unit circle. So the coordinate ring of the unit circle is the quotient ring RR[x,y]/(x²+y²-1).

(8/48)

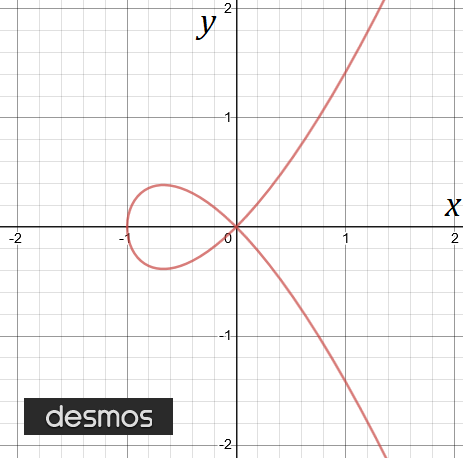
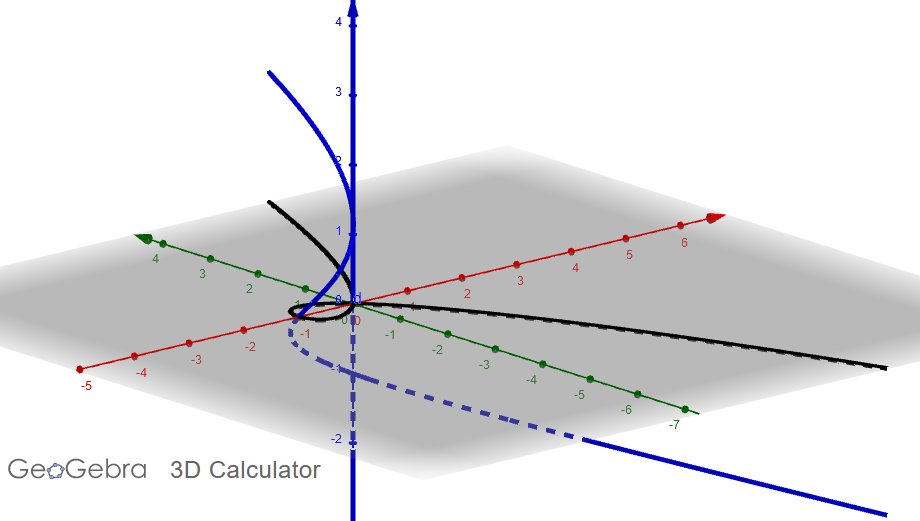
Now, let's turn our attention to a very interesting curve living in the real plane, the curve defined by y²-x³-x² = 0. There's one very interesting point on this curve - the origin is a node, a special type of singularity.

(9/48)

The reason there is a singularity at the origin is because the tangent space is messed up - there are two linearly independent tangent directions, rather than one like all the other points on the curve.

(10/48)

One big problem in algebraic geometry is the resolution of singularities. Can we find a curve which is, for all intents and purposes, "the same" as our original curve except that it has no singular points?

(11/48)

For our particular curve, we can imagine it as if it were a wire or piece of string living in 3-dimensional space. We can pull one part of the curve upward and push the other part of the curve downward, separating the singularity at the origin.

(12/48)

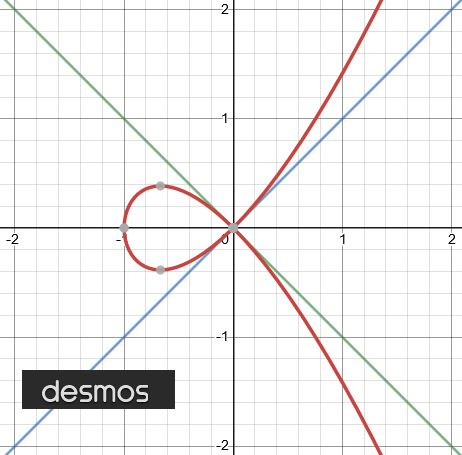
Another way to think about this is to think about pulling apart the curve along all lines passing through the origin.

Most - but not all (and this is important!) - of the lines passing through the origin can be parameterized as y=ux.

(13/48)

So, we can use the slopes of the lines to create a height above the plane. We get the collection of points (x,y,u) in RR³ satisfying both y²-x³-x² = 0 and y=ux simultaneously.

So the height of a point on our new curve is the slope of the line passing through it.

(14/48)

One crucial thing to note here is what happens when x=0 and y=0, the singular point on our original curve. Any u-value satisfies these two equations. As such, we should get the entire u-axis as well. So we get a curve *and* a line.

(15/48)

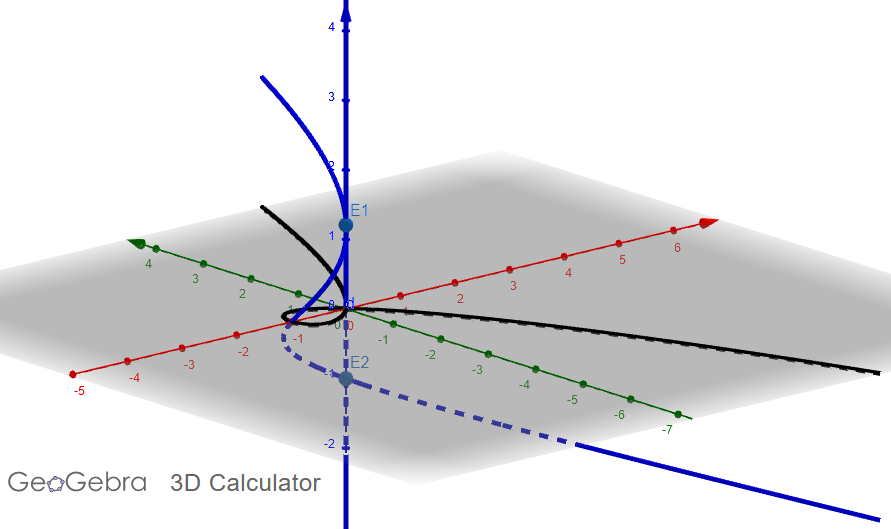
Notice that the u-axis intersects the other curve in exactly two points (labeled E1, E2). We can think of these two points as being what happens when we "pull apart" the origin in an attempt to get a nonsingular curve.

(16/48)

If we ignore this exceptional line for the u-axis, except for the intersection points E1 and E2, this new curve projects onto the original curve and is an isomorphism at every point *except* E1 and E2, where the projection is 2-to-1.

(17/48)

But as noted before, this doesn't quite work. y=ux does not capture all lines through the origin. Neither does x=uy. So instead of trying to capture all lines in affine space, we can use projective space.

(18/48)

Projective n-space is the collection of all lines passing through the origin in affine (n+1)-space. We can define projective n-space as a quotient of affine (n+1)-space minus the origin, where two points are equivalent if they lie on the same line through the origin.

(19/48)

So, projective 1-space (the projective line) can be given by projective coordinates [a:b], where a and b cannot both be simultaneously 0, and [a:b] = [λa:λb] for all nonzero λ. There is no point [0:0].

(20/48)

The important thing about the projective coordinates [a:b] are the ratios between the components. Essentially, the "points" in projective space are *directions* in affine space, which correspond to lines through the origin in affine space.

(21/48)

So instead of trying to parameterize all lines through the origin and associating points on the curve with slopes of these lines, we can instead associate points on the curve with points on the projective line (i.e., lines in the plane).

(22/48)

So we define the blowup of the curve at the origin as a subspace of RR²×P¹, where P¹ represents the projective line.

We get points (a,b,u) where (a,b) is not the origin and is on the curve, and where u is the point in P¹ corresponding to the line through (a,b).

(23/48)

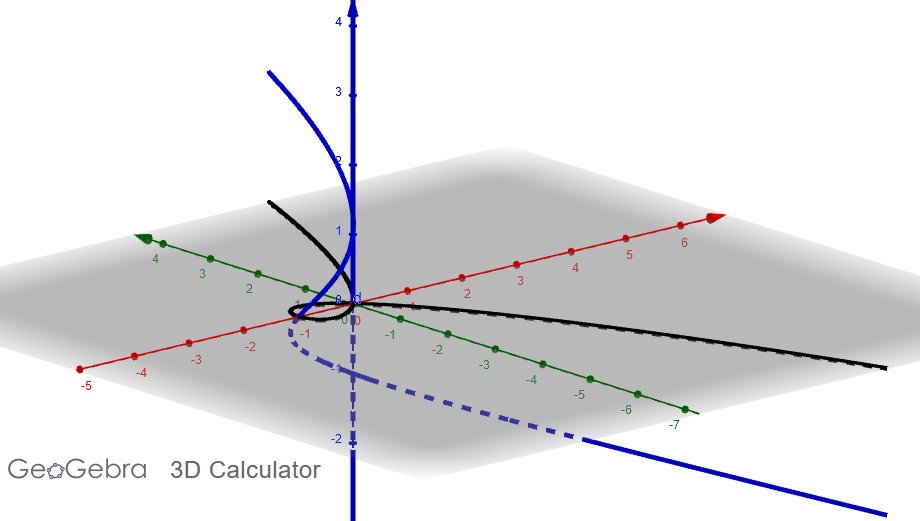
We also get the points (0,0,u) for *any* u in P¹. In other words, the origin is associated with the entire projective line. We can think of this as corresponding to the u-axis we got before when we were trying to pull the curve apart along parameterized lines in (15/48).

(24/48)

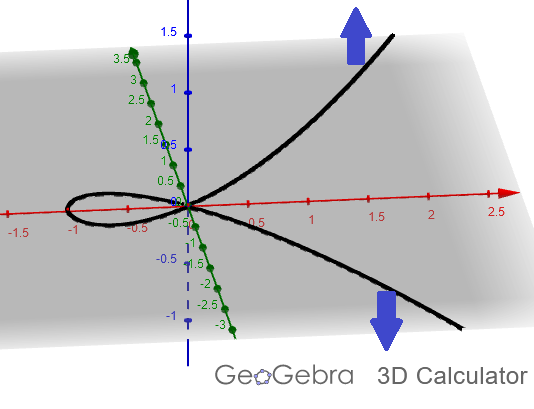
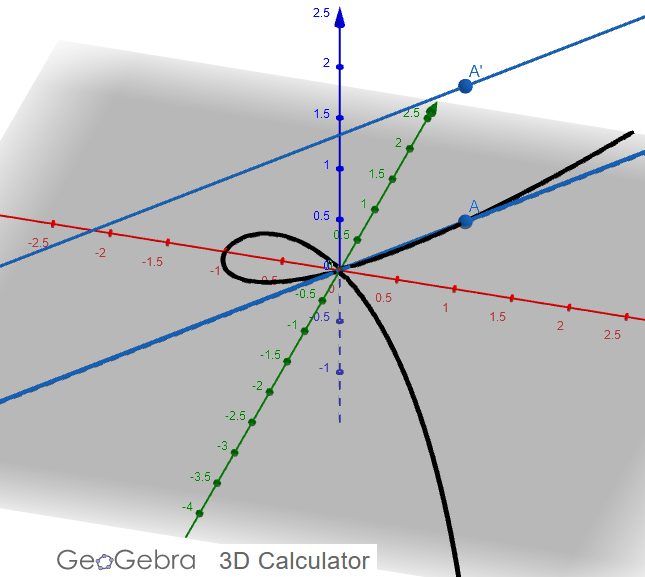
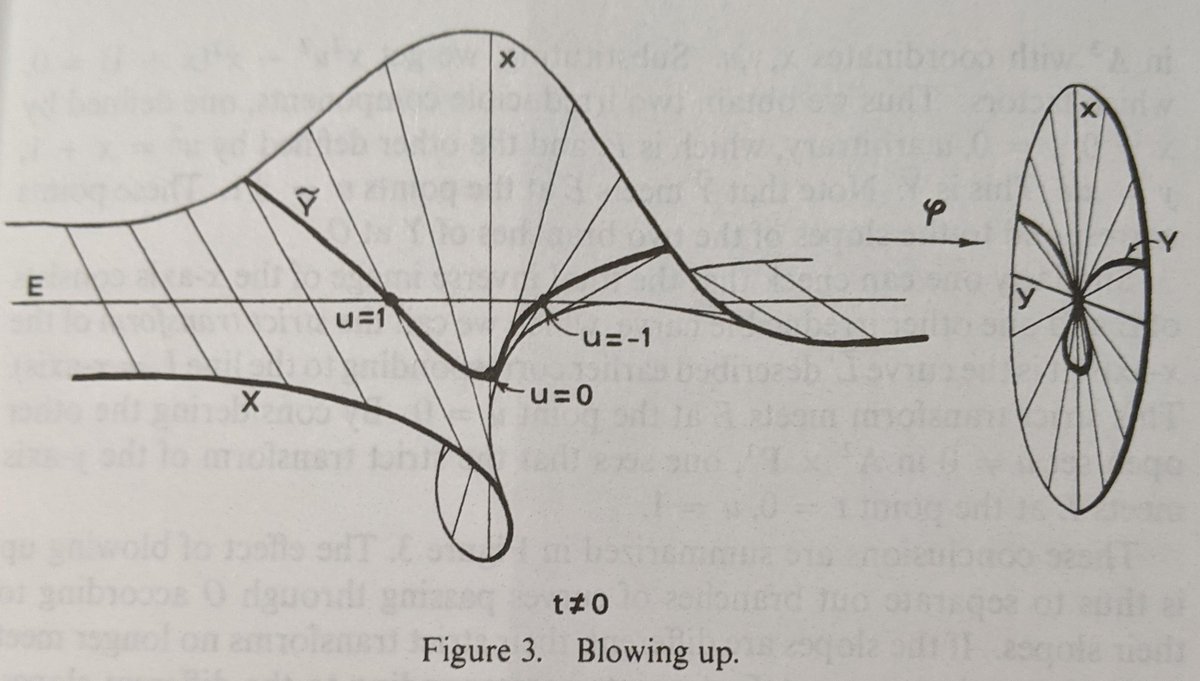
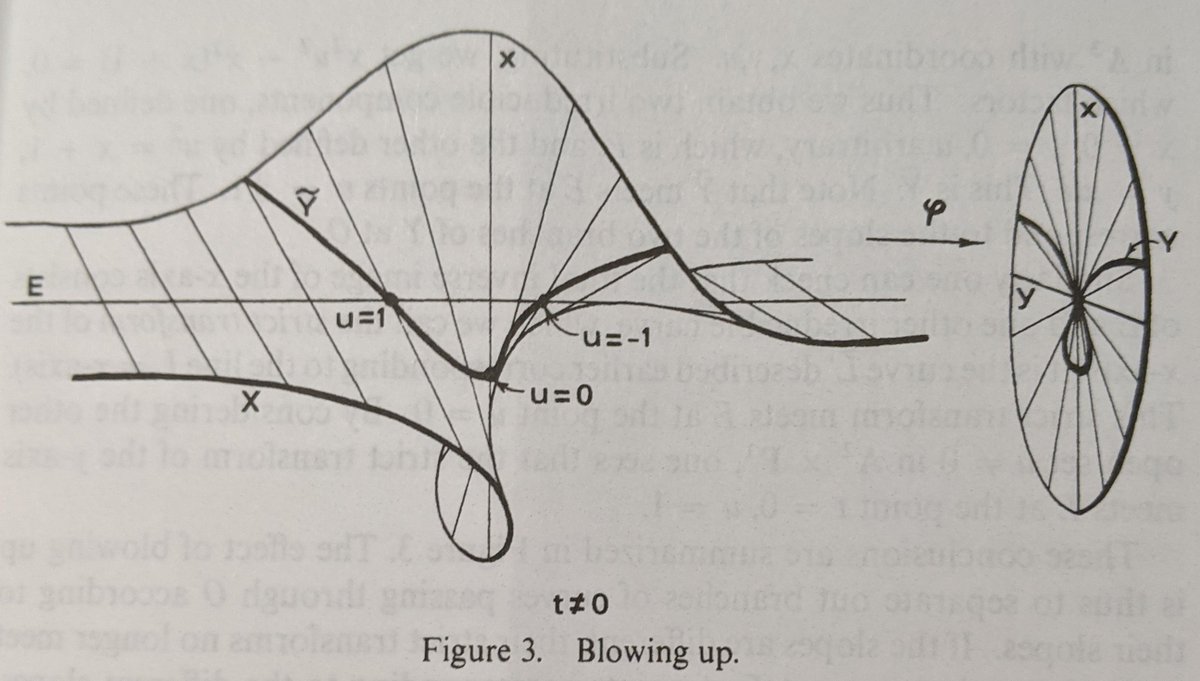
For the curve we have been focusing on, this leads us to this classic picture of the blowup at the origin, from Hartshorne page 29.

Y represents the curve, Y~ the blowup, E the projective line (E stands for "exceptional curve").

(25/48) Alt pic: Hartshorne

The blowup is nonsingular in this case, and it's isomorphic to our original curve *except* at the exceptional curve projecting to the point where we "blew it up".

This solves our problem of resolution of singularities (in this example).

(26/48)

Now, we can ask the following question: how can we study these blowups? Well, just like before, we want the coordinate ring of the blowup.

Let's turn back to our curve with the node at the origin. Let R denote the coordinate ring of this curve.

(27/48)

From (8/48), we saw R = RR[x,y]/(y²-x³-x²). Now, the blowup essentially includes our original curve, so we want to include R as part of our coordinate ring, but we want more functions than before! We want functions which have "poles" at the origin.

(28/48)

These "poles" account for the exceptional curve that "explodes" out of the origin when we pull apart our original curve. We can capture this by including a new variable t and allowing the functions xt and yt, since x=0 and y=0 defines the origin.

(29/48)

So we find that the homogeneous coordinate ring of the blowup should be R[xt,yt]. Said another way, if we denote the ideal corresponding to the origin as I (I = (x,y)), then the homogeneous coordinate ring of the blowup is R[It].

(30/48)

In general, given a coordinate ring R corresponding to an affine variety (shape) X and an ideal I corresponding to a subvariety (subshape) Y, the homogeneous coordinate ring of the blowup of X along Y is the ring R[It] as a subring of R[t].

(31/48)

(To see the above in a more formal setting, one uses schemes and the ideal sheaf; see Chapter II, Section 7 of Hartshorne. More specifically, page 163.

Also, thanks to @littmath for helping me with intuition on this.)

(32/48)

(As another aside, blowing up once doesn't guarantee a resolution of singularities. However, in 1964, Heisuke Hironaka proved that, in characteristic 0, singularities can be resolved by a finite sequence of blowups.)

(33/48)

The ring R[It] is called the Rees ring (or Rees algebra) of I (over R), named after David Rees. As we have already noted, the Rees ring is the homogeneous coordinate ring of the blowup. But there are pieces of the blowup which are very important.

(34/48)

The Rees ring R[It] is isomorphic as a graded ring to R
\\oplus I \\oplus I² \\oplus I³ \\oplus ... etc.,
i.e., the direct sum of the powers of I,where the degree d piece is represented by the d-th power of the ideal I.

(35/48)

One thing we care about is the exceptional fiber of the blowup. These are the points of the blowup that project onto the subshape along which we are blowing up. In the classic blowup picture, the exceptional fiber is given by the curve E.

(36/48)

To find the homogeneous coordinate ring of the exceptional fiber, we can again think about restricting our functions to just the exceptional set. Note that the exceptional set projects onto the points defined by our ideal I.

(37/48)

This means that the generators of the ideal I vanish on the subshape along which we are blowing up. Said another way, the generators of I are indistinguishable from the 0 function on the exceptional set.

(38/48)

Thus, we see that the homogeneous coordinate ring of the exceptional set should be the homogeneous coordinate ring of the blowup modulo the extension of I. In other words, R[It]/IR[It]. This ring is called the associated graded ring of I, and is sometimes denoted G(I).

(39/48)

The associated graded ring G(I) is isomorphic as a graded ring to
R/I \\oplus I/I² \\oplus I²/I³ \\oplus I³/I⁴ \\oplus ... etc.,
where the degree d piece is represented by the d-th power of the ideal I modulo the (d+1)st power of the ideal I.

(40/48)

Another part of the blowup one might care about is the special fiber. If the origin lives inside the shape you're blowing up, then you might care about what part of the blowup projects onto the origin. This is the special fiber of the blowup.

(41/48)

(Note: in our particular example of blowing up the curve given by y²-x³-x² = 0 at the origin, the special fiber is the same thing as the exceptional fiber. However, in general, you may not be blowing up along a subshape containing the origin.)

(42/48)

So what's the homogeneous coordinate ring of the special fiber? Well, we note that if we restrict to the special fiber, then the ideal corresponding to the origin is indistinguishable from the 0 function.

(43/48)

So let m denote the ideal corresponding to the origin (for example, if you're in F[x,y,z], the origin corresponds to m = (x,y,z), since the vanishing of all three coordinates is the origin).

(44/48)

Then the homogeneous coordinate ring of the special fiber is given by the ring R[It]/mR[It]. This is often denoted by F(I) and is called the "special fiber ring of I".

(45/48)

So we see that there are three important rings associated with blowups, the Rees ring R[It] (sometimes denoted R(I)), the associated graded ring G(I), and the special fiber ring F(I). These are the blowup algebras.

(46/48)

These blowup algebras are of great importance in a number of areas in algebraic geometry and commutative algebra, not just limited to the context of blowups.

In the future, I plan to showcase how these blowup algebras arise in other contexts as well.

(47/48)

So thank you for reading my very long thread! I hope it was understandable and interesting!

If I have made any mistakes (which I would be shocked if I hadn't), feel free to correct me!

(48/48)

EXERCISE: In the classical picture of a blowup from Hartshorne, we get a kind of "twisted" surface that the blowup lives on. This represents the blowup of the real plane at the origin. Convince yourself that the blowup of the plane at the origin is a (noncompact) Möbius band.