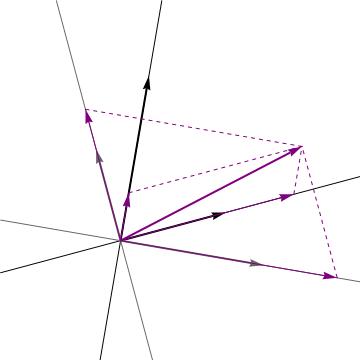
Co- and contra-variant components of a vector: given a vector v in a finite-dimensional inner product space (V,⋅), we would like to calculate its components wrt a given basis B = {e₁,e₂,…eₙ}. If B is orthonormal, this is easy: the ith componenth of v is vⁱ = v ⋅ eᵢ (1/10)
If B is not orthonormal but merely orthogonal, this is still not so bad, the components are given by vⁱ = v ⋅ eᵢ / (eᵢ ⋅ eᵢ), i.e. we just have to account for the squared norm of the basis vectors (2/10)
However, if B is not even orthogonal then the process is more involved. To solve this problem, we introduce the concept of a *reciprocal basis*. The idea is this: having fixed the basis, the ith component of a given vector is linear functional on V, right? Right. (3/10)
So the ith component of v, like any linear functional, ought to be given by taking the dot product of v with some vector eⁱ (note the super/subscripts), even if eⁱ ≠ eᵢ. (4/10)
We should expect, given our objectives for this vector, that eⁱ ⋅ eᵢ = 1 but eⁱ ⋅ eⱼ = 0 whenever i ≠ j, which is sufficient to uniquely determine the vector eⁱ. The collection B' = {e¹,e²,…,eⁿ} is then referred to as the *reciprocal basis* for B. (5/10)
It is not hard to show that B' is linearly independent and spans V, and likewise to see that the relation of two bases being reciprocal to each other is symmetric (ie if A = B' then B = A'). (6/10)
Having found that vⁱ = v ⋅ eⁱ, we refer to the components so determined as the *contravariant components* of v. Since we've got a nice new basis lying around, we may as well express v wrt B', these components are given by vᵢ = v ⋅ eᵢ (again, look at the scripts) (7/10)
These comps of v wrt B' are called the *covariant components* of v, *with respect to B*.
Let's reiterate that.
The contravariant components of v wrt B are the coeffs of the expansion of v wrt B, while the covariant components wrt B are the coeffs of the exp of v wrt B' (8/10)
Let's reiterate that.
The contravariant components of v wrt B are the coeffs of the expansion of v wrt B, while the covariant components wrt B are the coeffs of the exp of v wrt B' (8/10)
Now the reason these are called covariant and contravariant, is its own thread which I am not yet ready to write at the moment. Suffice it to say that if you happen to know any category theory and have not yet come across these things you will not be happy. (9/10)
The picture that I have above depicts the expansion of a vector with respect to a particular basis (black) and its reciprocal basis (gray). I find it much easier to comprehend things when I have a visual representation of what I'm studying. (10/10).

 Read on Twitter
Read on Twitter