Read on Twitter
Stuff I wish I had known sooner: "Pinsker's inequality is cancelled," a thread. 
If you want to relate total variation (TV) and Kullback-Leibler divergence (KL), then everyone, from textbooks to Google, will point you to Pinsker's inequality: TV(p,q) ≤ √(½ KL(p||q) )
1/
If you want to relate total variation (TV) and Kullback-Leibler divergence (KL), then everyone, from textbooks to Google, will point you to Pinsker's inequality: TV(p,q) ≤ √(½ KL(p||q) )
1/
It's warranted: a great inequality, and tight in the regime where KL→0. Now, the issue is that KL is unbounded, while 0≤TV≤1 always, so the bound becomes vacuous when KL > 2. Oops.
2/
*I'm using it with the natural log, by the way, so no pesky log 2 constants.
2/
*I'm using it with the natural log, by the way, so no pesky log 2 constants.
This is annoying, because in many situations, you would want to bound a TV close to 1: for instance, in hypothesis testing: "how many samples to distinguish between an ε-biased and a fair coin, with probability 1-δ?"
Well, you'd like to start bounding 1-δ ≤ TV ≤ ?.
3/
Well, you'd like to start bounding 1-δ ≤ TV ≤ ?.
3/
Here's the kicker: nobody ever told me,* but there is a simple bound that works in the regime KL≫1! A bound that is always non-vacuous, and goes to 1 as KL→∞.
*I mean, a paper did by referencing Tsybakov's "Introduction to Nonparametric Estimation": https://arxiv.org/abs/2009.06540
4/
*I mean, a paper did by referencing Tsybakov's "Introduction to Nonparametric Estimation": https://arxiv.org/abs/2009.06540
4/
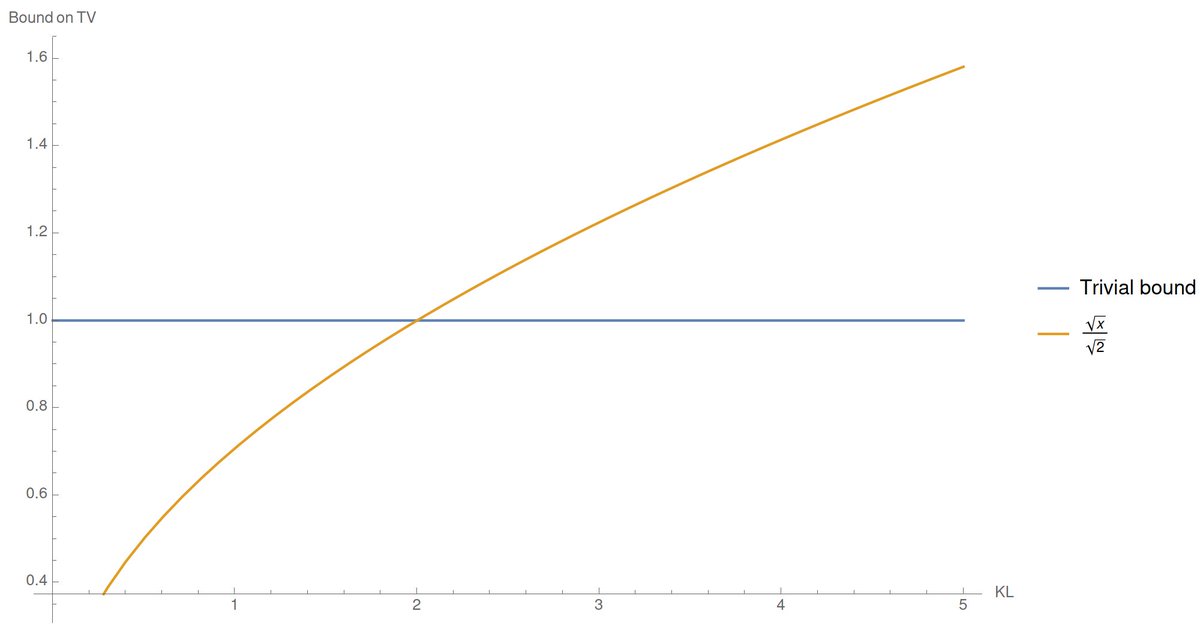
Cool. So now, here's what we get: we can take the minimum of what Pinsker's and this new inequality give to get the bound in red, which objectively is pretty nice and useful everywhere.
Are we done? No. Maybe we don't have to consider these two bounds separately?
5/
Are we done? No. Maybe we don't have to consider these two bounds separately?
5/
So, let's see Tsybakov's proof. It's short, but it uses Jensen's so *clearly* we can't trust it. Nope.
Tsybakov credits the inequality to Bretagnolle and Huber (1979), so let's look at those and see if they don't prove something a bit tighter?
6/
Tsybakov credits the inequality to Bretagnolle and Huber (1979), so let's look at those and see if they don't prove something a bit tighter?
6/
Here, for the faint of heart: fly, you fools! It's from the pre- #LaTeX times, when people were people and wrote their formulae BY HAND. https://twitter.com/ccanonne_/status/1339293813890695169
Also, in French.
Anyways, all the action is in Lemma 2.1, and more specifically its proof.
7/
Also, in French.
Anyways, all the action is in Lemma 2.1, and more specifically its proof.
7/
So, here's the new bound we have, if I can parse this freaking proof correctly (pardon my... French?).
It's always at least as good as the bound by Tsybakov, since that used the inequality √(1-exp(-x)) ≤ 1-(1/2)exp(-x) on top of it. But it behaves much better as KL→0.
8/
It's always at least as good as the bound by Tsybakov, since that used the inequality √(1-exp(-x)) ≤ 1-(1/2)exp(-x) on top of it. But it behaves much better as KL→0.
8/
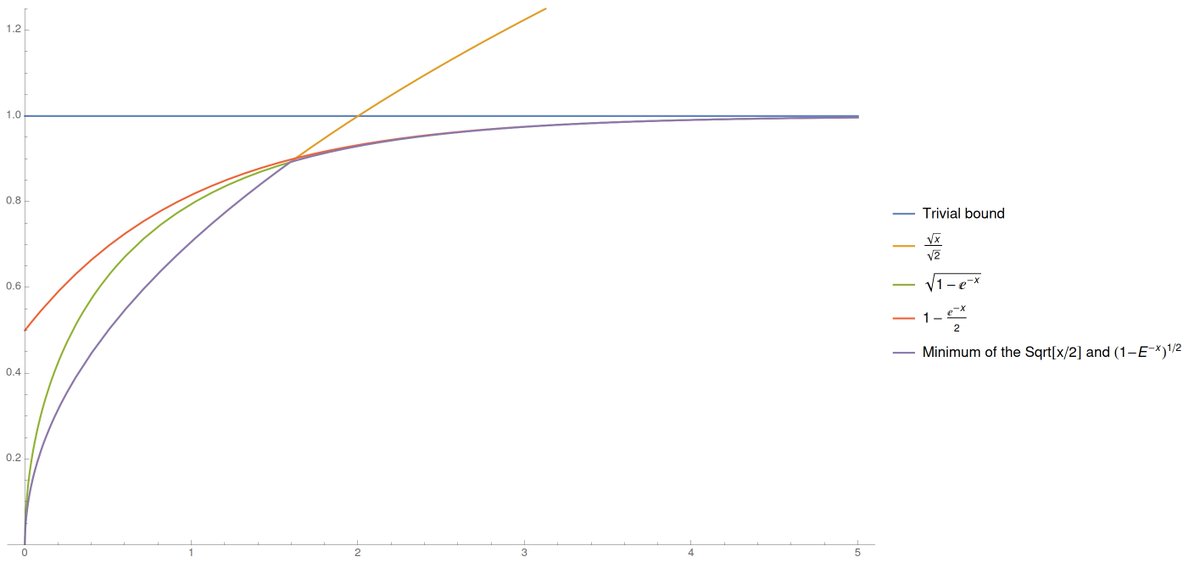
So here the current state. The green curve is the new inequality we have, which, OK, is not as tight as it gets everywhere (sometimes Pinsker's is still better)...
But is it? One can easily check that our new bound (which, again, is non-vacuous for *all* values of KL) is...
9/
But is it? One can easily check that our new bound (which, again, is non-vacuous for *all* values of KL) is...
9/
... always within a √2 factor of what Pinsker's inequality would give. Big deal...
So, summary: forget Pinsker's, we have better (unless you really care about constants, but then, who are you?).
And again, *why did I not know this before*?
10/
So, summary: forget Pinsker's, we have better (unless you really care about constants, but then, who are you?).
And again, *why did I not know this before*?
10/
To conclude, 2 points:
(1) As @mraginsky pointed out, bounds tighter than Pinsker's are known and discussed in some places. E.g., Yihong Wu's notes (again), Section 5.2.2 have some... but I find it much harder to parse, and it never actually clicked.
http://www.stat.yale.edu/~yw562/teaching/it-stats.pdf
11/
(1) As @mraginsky pointed out, bounds tighter than Pinsker's are known and discussed in some places. E.g., Yihong Wu's notes (again), Section 5.2.2 have some... but I find it much harder to parse, and it never actually clicked.
http://www.stat.yale.edu/~yw562/teaching/it-stats.pdf
11/
(2). Thomas Steinke ( @shortstein) mentioned that Pinsker's can be derived from "the best inequality" (combined with Hoeffding's lemma). Can this new, amazing inequality be derived from it as well?
12/
12/
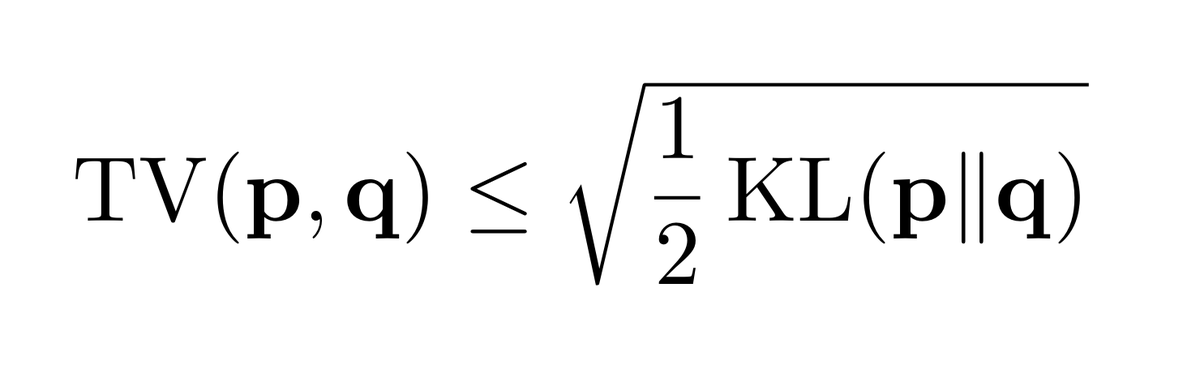
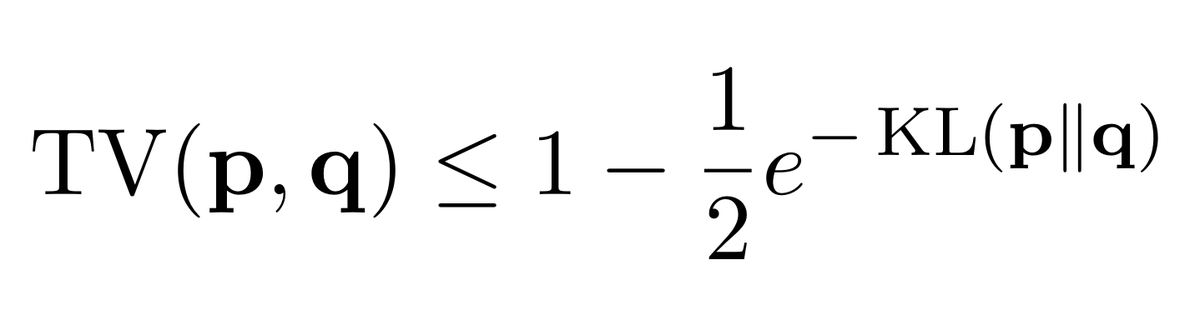
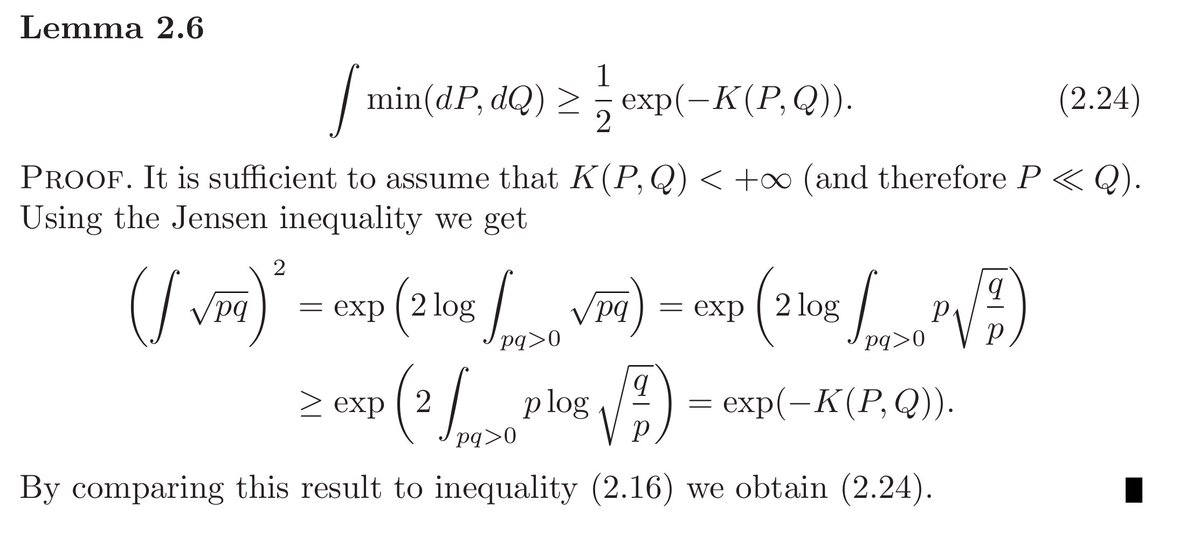
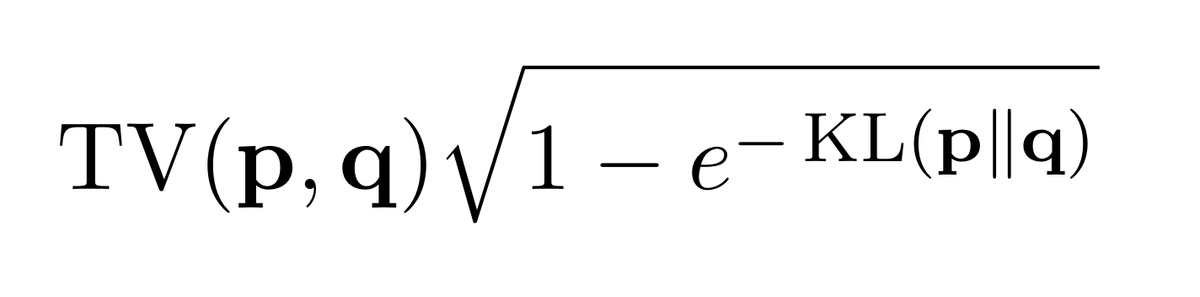
Finally, going to write the inequality (and its weaker form given in [Tsybakov09]) again. It is always better than Pinsker's, up to a √2 factor at worst, and *significantly* better in the regimes KL≥2 and KL→∞ where Pinsker's is vacuous.
As I said, Pinsker is cancelled.
/end
![Finally, going to write the inequality (and its weaker form given in [Tsybakov09]) again. It is always better than Pinsker's, up to a √2 factor at worst, and *significantly* better in the regimes KL≥2 and KL→∞ where Pinsker's is vacuous.As I said, Pinsker is cancelled./end](https://pbs.twimg.com/media/EpZPJHKU0AIoVjc.png "Finally, going to write the inequality (and its weaker form given in [Tsybakov09]) again. It is always better than Pinsker's, up to a √2 factor at worst, and *significantly* better in the regimes KL≥2 and KL→∞ where Pinsker's is vacuous.As I said, Pinsker is cancelled./end")
As I said, Pinsker is cancelled.
/end
