Finding geodesics on triangle meshes is a classically tricky problem. In new work with @keenanisalive at SIGGRAPH Asia, we discovered that a simple policy of greedily flipping edges provably generates a geodesic path! (1/N)

https://nmwsharp.com/research/flip-geodesics/

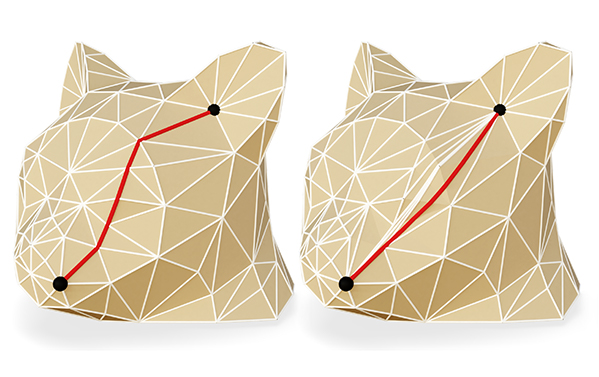
Geodesics are like straight lines, or locally-shortest paths along a shape. Our algorithm takes a path along the edges of a mesh, and "pulls it tight" to an exact geodesic. (2/N)

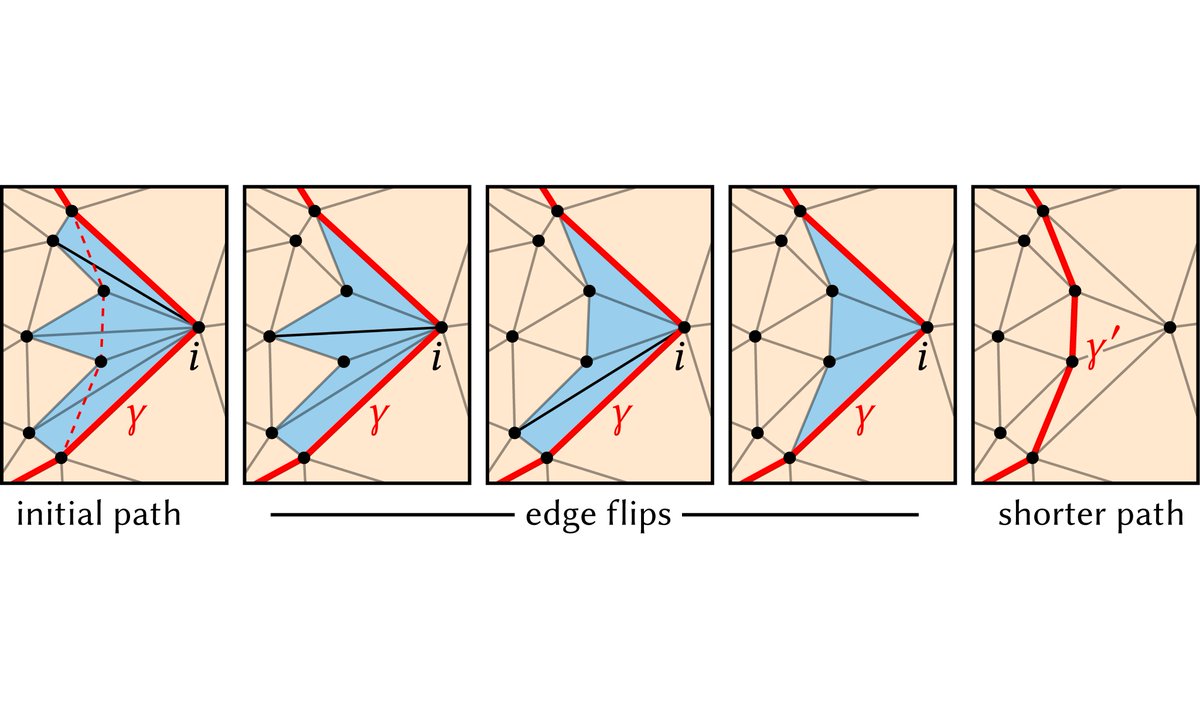
The core observation is that if a curve is not yet a geodesic, you can "flip out" edges in a vertex neighborhood to introduce a shorter path. We prove that this _always_ works, and apply it with intrinsic edge flips on surfaces. (3/N)

Once we have a subroutine that provably makes the path shorter in a local region, we can just apply it repeatedly until the path is a geodesic.

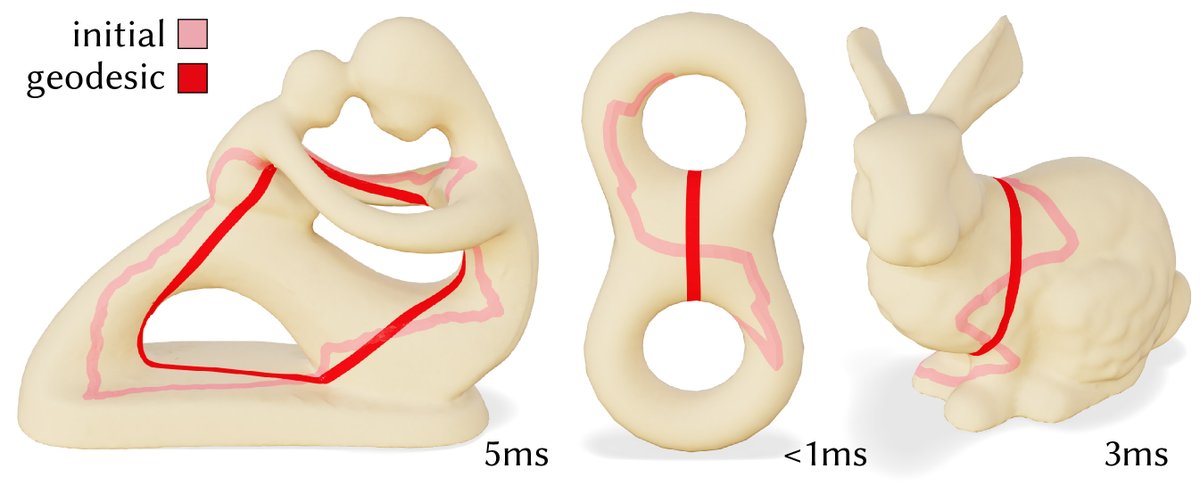
The same basic procedure generalizes immediately to loops, or even networks of paths and loops along a surface. (4/N)

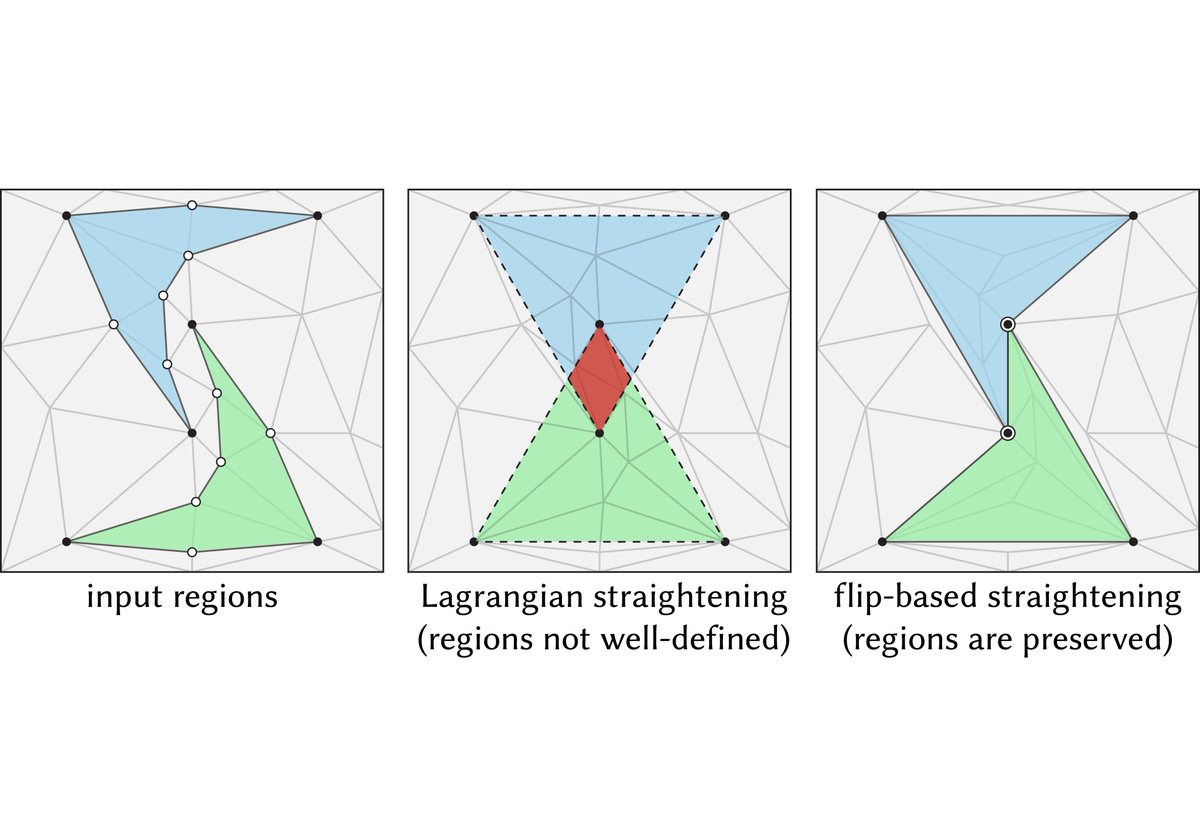
This approach offers a powerful new property: it guarantees that curves will not cross during shortening. Formally, we find a geodesic in the same isotopy class input. (5/N)

This non-crossing property is critical for applications like straightening cut graphs in computational fabrication, or segmentation boundaries, where allowing curves curves to cross would destroy the notion of patches along the surface. (6/N)

Shortening a given curve to a geodesic is much faster than e.g. finding globally shortest geodesics---our procedure takes just a few milliseconds even on huge meshes, and is on-average 10x faster than just running Dijkstra's algorithm between the endpoints. (7/N)

Even better, edge flips don't just generate geodesics, they generates a triangulation conforming to these geodesics, akin to constrained Delaunay triangulation in the plane.

This makes it easy to do things like use geodesics as boundary conditions for PDEs. (8/N)

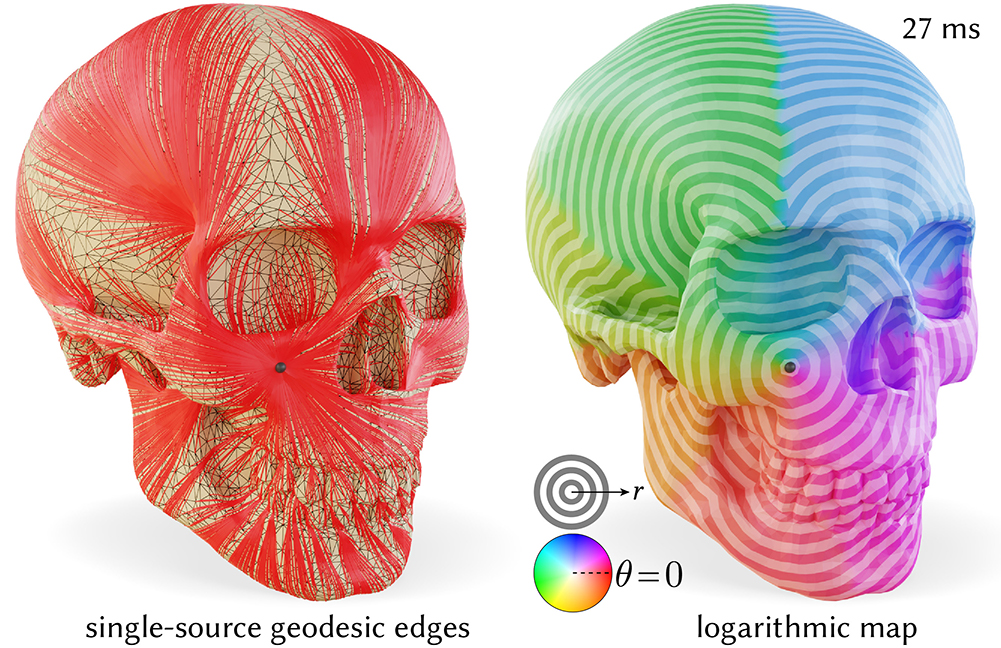
We also show an example finding locally-shortest geodesics from a source, by flipping edges while running Dijkstra.

Amazingly, this implies that an intrinsic triangulation always exists which contains a geodesic path along edges from a source to each other vertex. (9/N)

Hear more in the "Meticulous Meshes" panel at SIGGRAPH Asia, 11pm EST on Sat. (fin)

- project: https://nmwsharp.com/research/flip-geodesics/
- paper: https://nmwsharp.com/media/papers/flip-geodesics/flip_geodesics.pdf
- code (library): http://geometry-central.net/surface/algorithms/flip_geodesics/
- code (demo app): https://github.com/nmwsharp/flip-geodesics-demo
- talk: [will be posted after SIGAsia!]