The gradient is a locally greedy direction. Where do you get if you follow the eigenvectors of the Hessian instead? Our new paper, “Ridge Rider” ( https://papers.nips.cc/paper/2020/file/08425b881bcde94a383cd258cea331be-Paper.pdf), explores how to do this and what happens in a variety of (toy) problems (if you dare to do so),.. Thread 1/N

..including zero-shot coordination, RL and causal learning. Instead of the gradient, RR follows all eigenvectors of the Hessian w/ negative eigenvalue ("Ridges"). As we show, starting from a saddle these ridges provide an orthogonal set of locally loss reducing directions..2/N

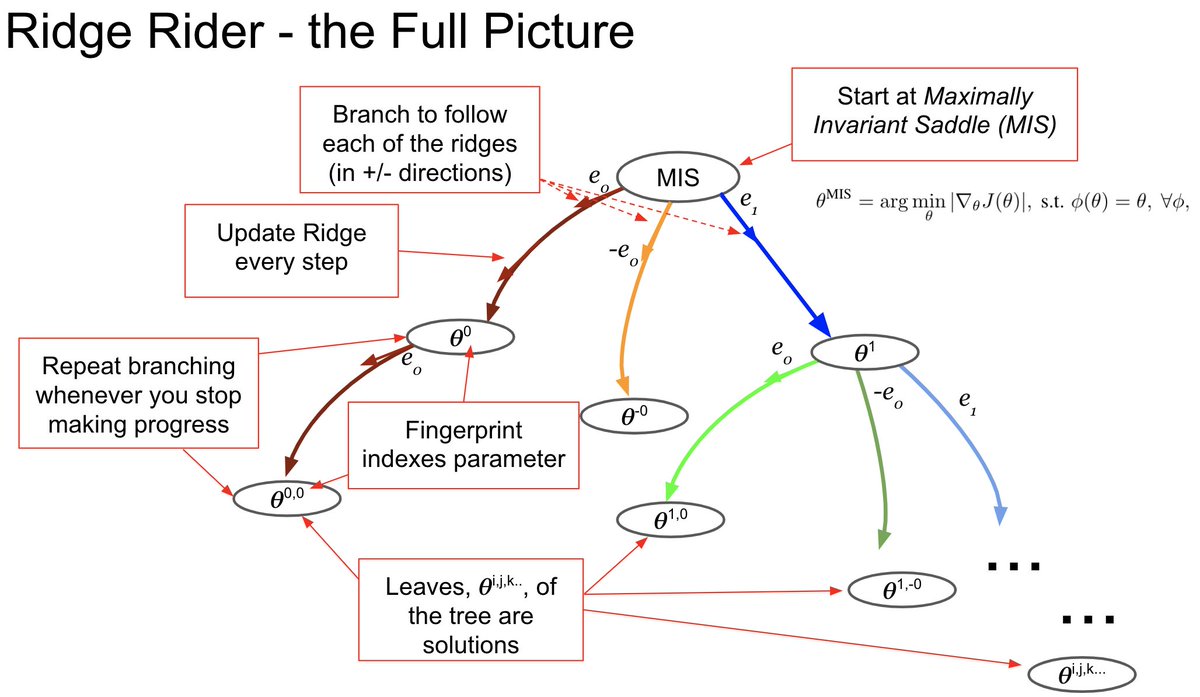
So how does it work? We begin by finding a special point in parameter space (Maximally Invariant Saddle), which has small gradient norm and respects all the symmetries of the underlying problem (in RL this is the maximum entropy saddle) .. 3/N

From the MIS we branch to explore the ridges by following the smooth continuation of each of the ridges after each update step. By repeating the branching process whenever we stop making progress we produce an entire tree of solutions which can be explored BF or DF. 4/N

Following different ridges leads to distinct regions of the parameter space, corresponding to different features/policies. Thus, RR is able to find solutions that are difficult or impossible to learn with SGD and the eigenvalues provide a natural indexing and grouping scheme. 5/N

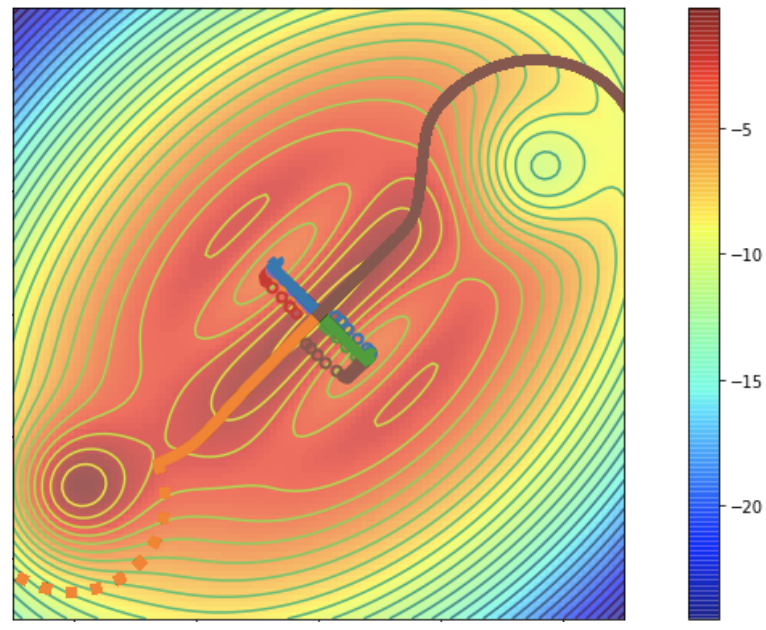
Below we see a 2d cost surface, where we begin in the middle (near the saddle) and want to reach the blue areas of low cost. SGD (circles) gets stuck in the valleys which correspond to the locally steepest descent direction. 6/N

When running RR, the first ridge also follows this direction, as we see in blue and green. However, the second, orthogonal direction (brown and orange) avoids the local optima and reaches the low value regions. More experiments are in our blog post: https://bair.berkeley.edu/blog/2020/11/13/ridge-rider/ 7/N

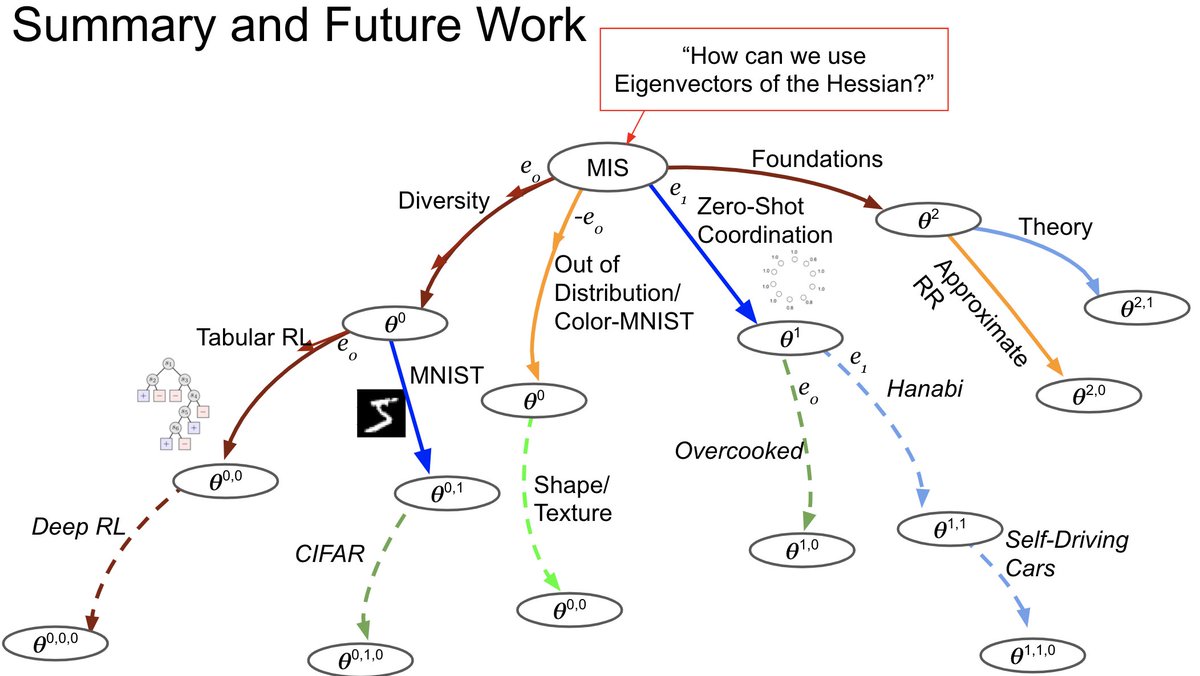
We are particularly excited to see early promise of RR in a variety of seemingly unrelated domains. We believe that symmetries/invariances and their connection to the Hessian play a crucial, but under-explored, role. 8/N

While expensive, we introduce ways to make this tractable, such as using Hessian-vector-products for approximate updates of the ridges, but there is still a long way to go. To help, the code is linked out from the paper and most experiments can be reproduced in the browser. 9/N

Since you are still reading, why not come visit us at our NeurIPS poster session next week: ( https://neurips.cc/virtual/2020/public/poster_08425b881bcde94a383cd258cea331be.html) and/or send comments & questions our way. Happy exploring! 10/N. N=10.
.