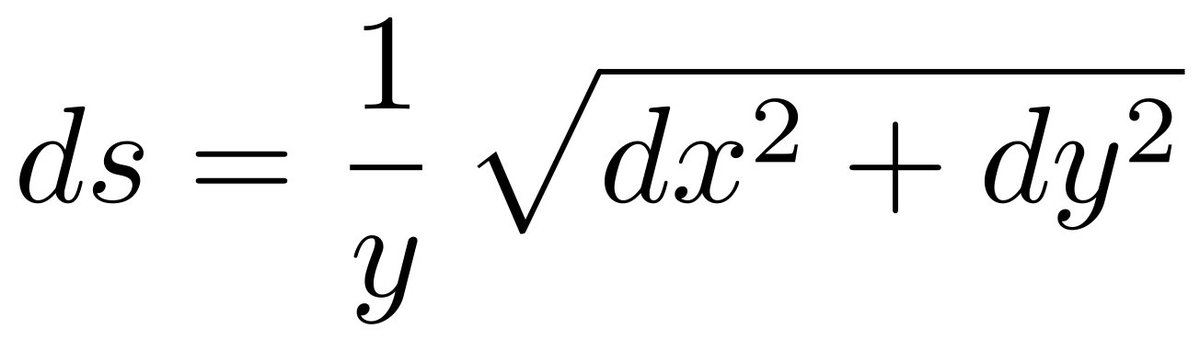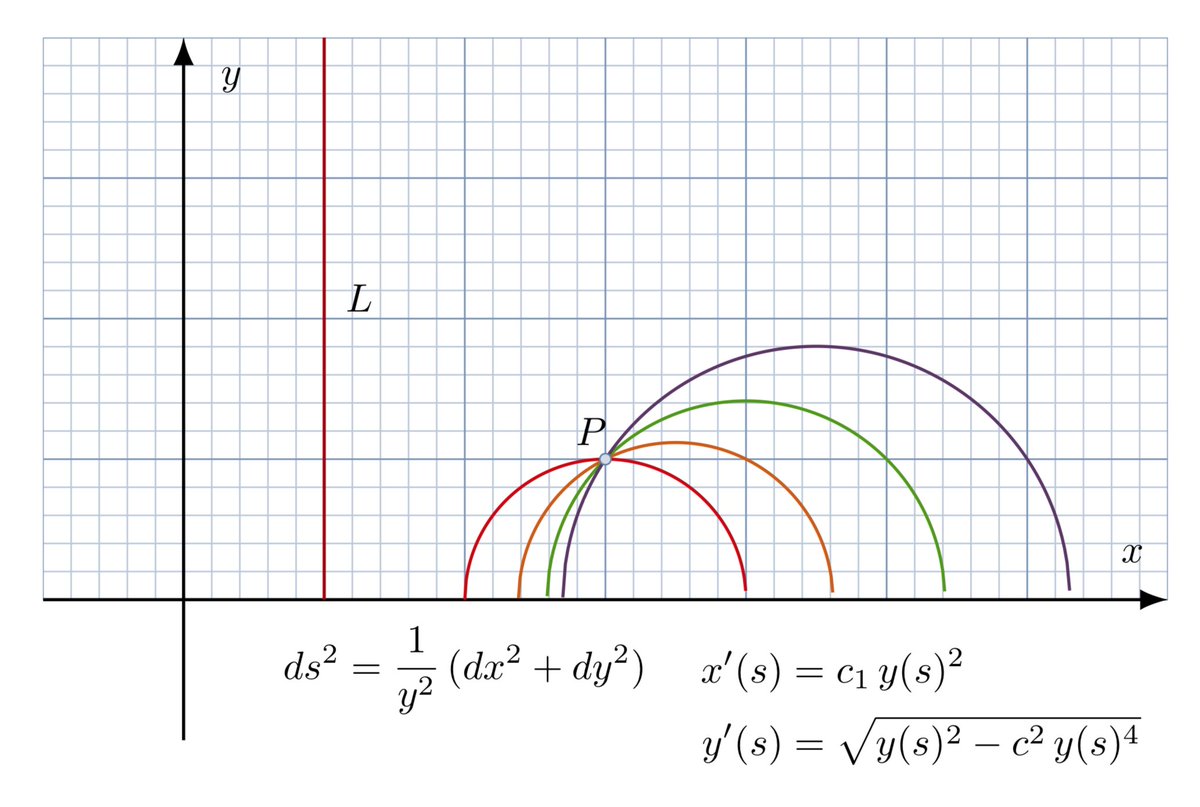The mathematician Nikolai Ivanovich Lobachevsky was born #OTD in 1792. He developed a non-Euclidean geometry that shows up in areas ranging from relativity to the designs of M.C. Escher.
Portrait: Lev Kryukov (wikimedia)

In Lobachevsky's geometry there exists more than one line parallel to a given line and passing through a point not on that line. Although the term "Lobachevsky geometry" is still used, we more frequently refer to it as "hyperbolic geometry" –– a term introduced by Felix Klein

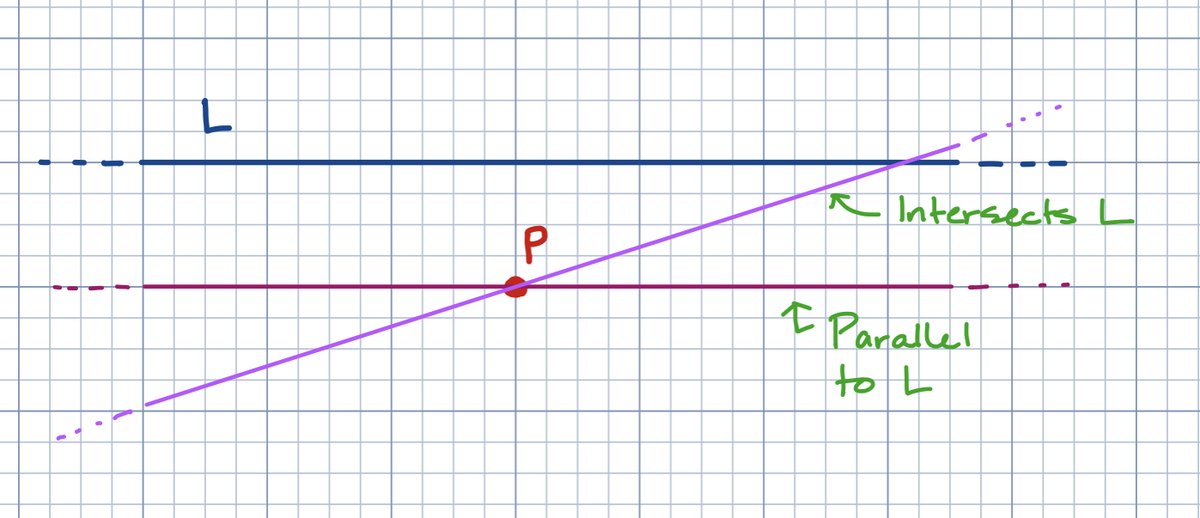
In Euclid's geometry, if you have a line L and a point P that is not on L, then there is exactly one line through P that does not intersect L. That line is parallel to L.

On a curved surface this isn't necessarily true. There, the generalization of a straight line is a "geodesic."

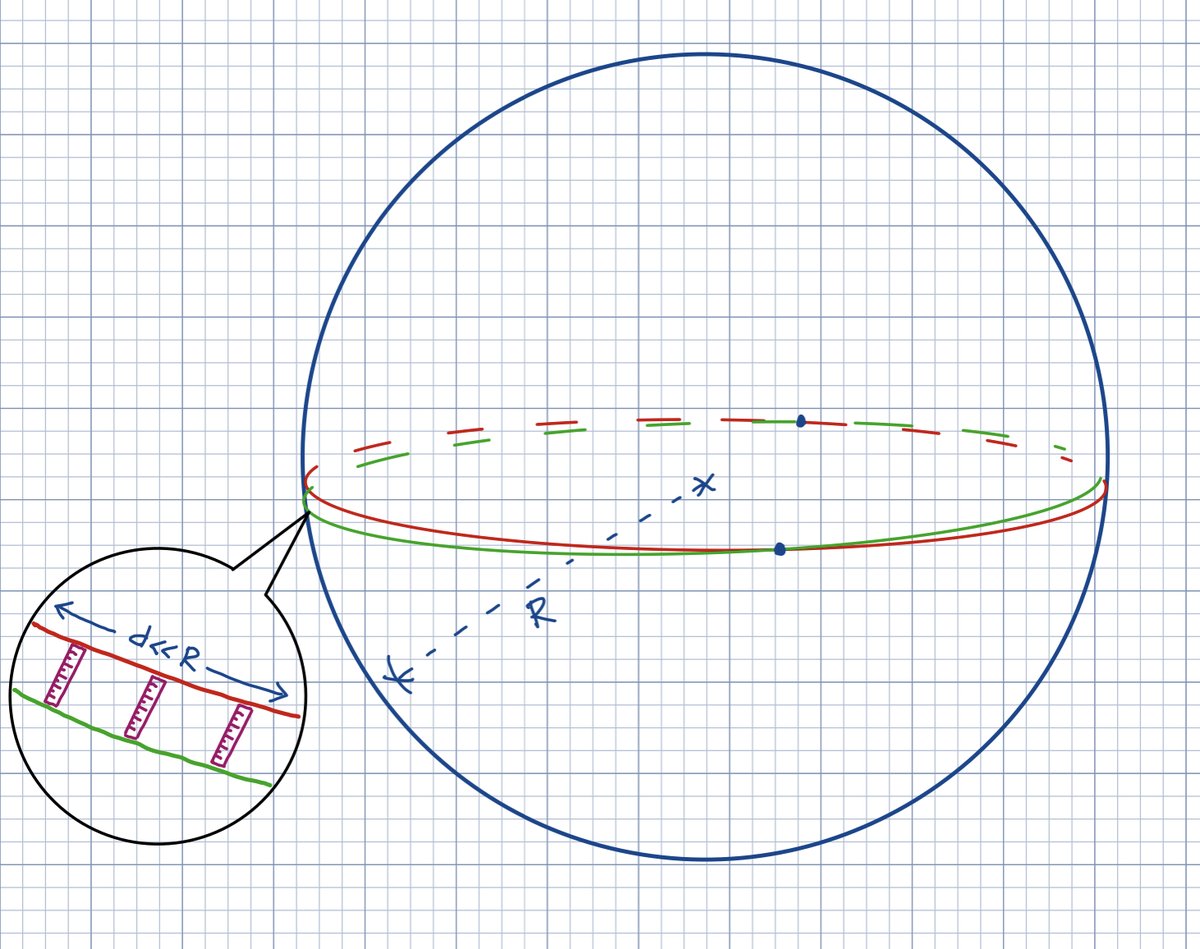
For example, the geodesics on a sphere are "great circles" (circles with the same circumference as the equator). Any two great circles intersect. So on the surface of a sphere, if you pick a "straight line" L and a point P not on L, then any straight line through P intersects L.

(Okay, before I go any further I am declaring a moratorium on Tom Lehrer references.)

On a curved surface, things look more or less flat over short distances –– you don't notice the curvature of the Earth standing in your front yard. On those scales ("locally") geodesics resemble the straight lines of Euclid's geometry.

But even though two geodesics on the surface of a sphere may look parallel over a short distance, they will eventually intersect if you follow them far enough. On larger scales –– in this case, distances comparable to the radius of the sphere –– the curvature is apparent.

Anyway, the type of geometry studied by Lobachevsky is the opposite: Given a straight line L (a geodesic) and a point P not on L, there are an infinite number of geodesics that pass through P but never intersect L.

There is a simple (but very important) example of this known as the Poincaré Upper Half-Plane. Despite the name, it was (afaik) first studied by the Italian mathematician Eugenio Beltrami.

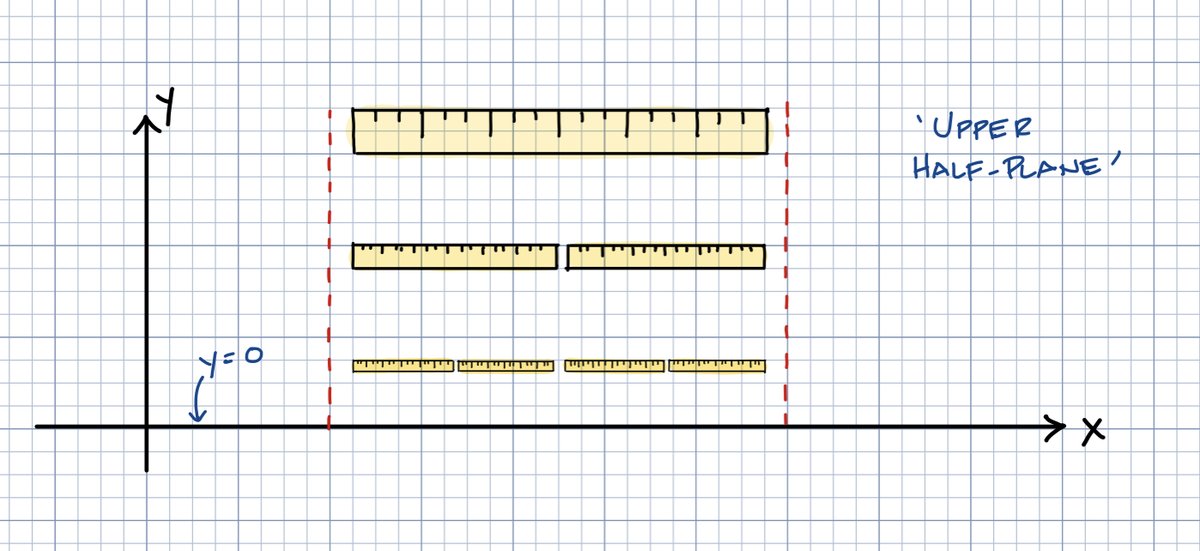
First, you take the x-y plane and ignore the bottom half. So it's all the points -∞ < x < ∞ and 0 < y < ∞. Then, you introduce a special rule for the distance between points. Here's where it gets a little weird.

As you get closer to the x-axis (y=0) your rulers get shorter and shorter, so that the distances you measure get longer and longer.

If two nearby points are dx apart in the x-direction, and dy apart in the y-direction, then the distance between them is:

As a result, you get two kinds of geodesics. Either straight vertical lines that take you between two points with the same x-coordinate, or semi-circles centered on the x-axis.

This makes sense: Geodesics are supposed to be something like (locally) shortest paths. So to go from A to B you should always veer away from the x-axis towards larger values of y where your rulers aren't so short.

And this means that given a straight line L like the vertical geodesic shown here, and a point P not on L, there are an infinite number of semicircle geodesics that pass through P but never intersect L. It's an unusual geometry!

But you have actually seen it before. It can be mapped onto a disk (the "Poincaré disk") by a Möbius transformation, which preserves relationships between straight lines. The x-axis becomes the edge of the disk.

The geometry of this Poincaré disk inspired Escher's "Circle Limit" drawings. In this case the rulers are the fish-lengths. See how they get small as you approach the edge?
Image: M.C. Escher, "Circle Limit III"

Hyperbolic geometry shows up all over the place in physics, especially in relativity. The Poincaré models described above are actually relevant for the AdS/CFT correspondence, as they describe a patch of (Euclidean) anti de Sitter space.

If you are curious about the relationship between AdS and hyperbolic geometry, and you've got some math under your belt, I strongly recommend Ingemar Bengtsson's ~beautiful~ lectures on Anti de Sitter space.
http://3dhouse.se/ingemar/Kurs.pdf

The diagram of geodesics in the upper half plane was made with tikz/pgf in LaTeX, here's the source: https://gist.github.com/mcnees/c8e9840c39c5d9202a509c46c2ad4c91