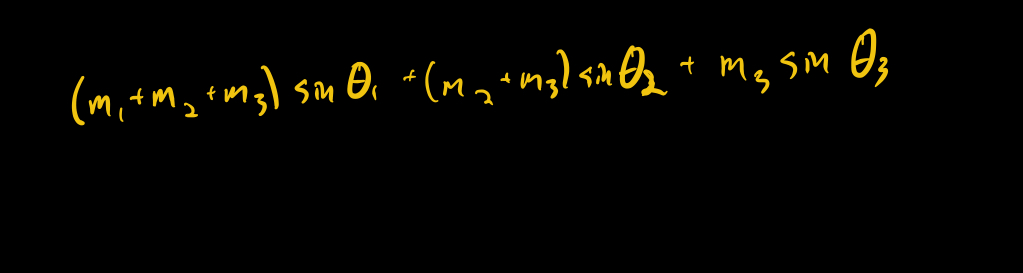A thread on the equilibria of pendulums and their connection to topology. 1/n

Consider the following physical system—an n-uple pendulum. This is a bunch of rigid rods connected at ball and socket joints, each of which has a weight, and pinned in place at the top. 2/n

What are the equilibrium positions of this pendulum? That is, what are the positions where the pendulum won’t move at all under the influence of gravity? 3/n

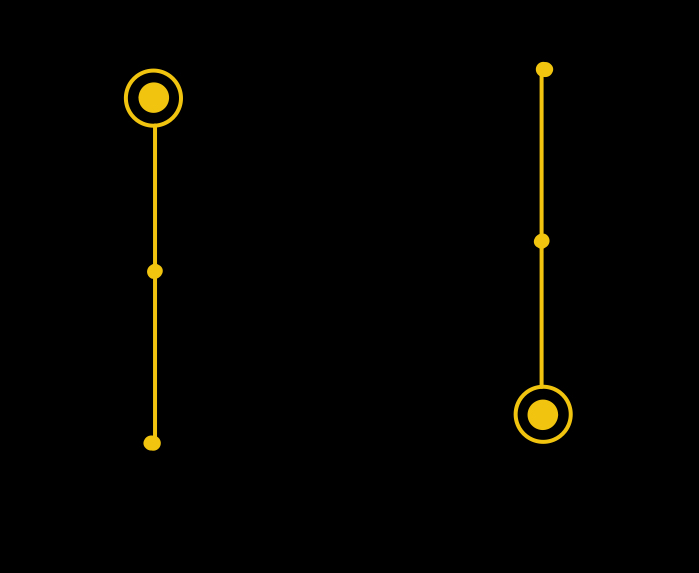
The equilibria occurs when all the rods are pointing either straight up or straight down. In the case of a double pendulum, with two rigid rods connected at a joint, I’ve drawn the four equilibria below. 4/n

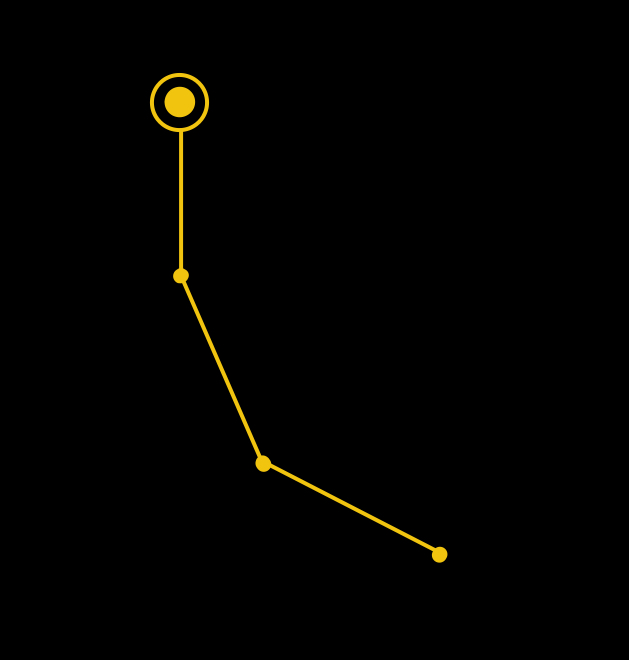
Not all equilibria are created equal. In the equilibrium where both rods are pointed straight downwards, the pendulum will tend to return to this equilibrium after a small perturbation. 5/n

On the other hand, if both rods are pointed straight up, the equilibrium is very precarious — any perturbation will cause the pendulum to collapse. 6/n

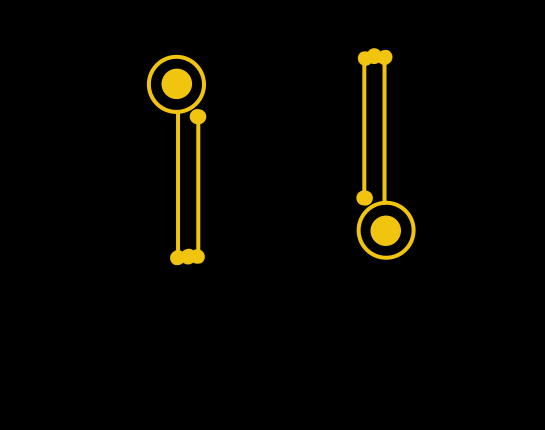
The other two equilibria are a bit more interesting — most perturbations will cause the pendulum to collapse, but in each case there’s one direction in which one can perturb the pendulum after which it will tend to return to the starting point. 7/n

Here’s a picture in the one of these two “one up, one down” equilibria. Note that it almost balances before collapsing. 8/n

And here’s the other one:

9/n

So there was one stable equilibrium, one totally unstable equilibrium, and two equilibria that were stable in one direction but unstable for most directions. 10/n

In general (with an n-uple pendulum) the equilibria are exactly the configurations where all the rods are pointing straight up or straight down. As there are n rods and each can be up or down, there are 2^n equilibria. 11/n

The equilibria with k stable directions are precisely the configurations where exactly k rods are pointing down and n-k rods are pointing up. There are (n choose k) of these. 12/n

I claim this fact is a reflection of some underlying topology. Namely, the topology (or shape) of the “configuration space” of the n-uple pendulum. 13/n

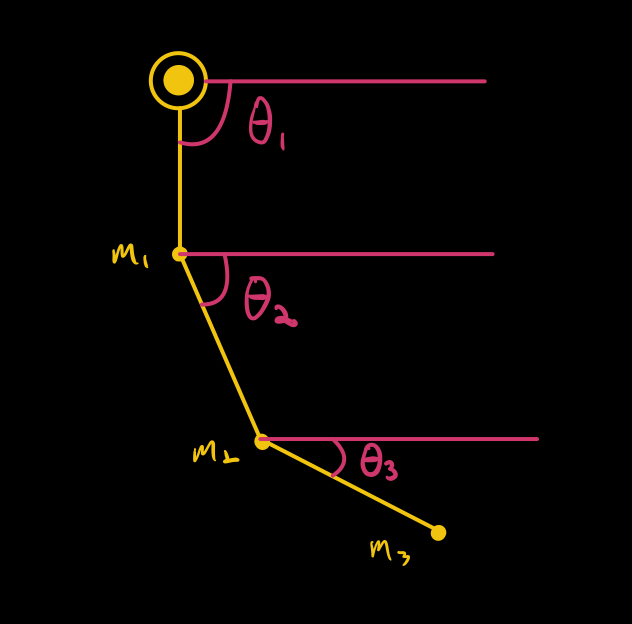
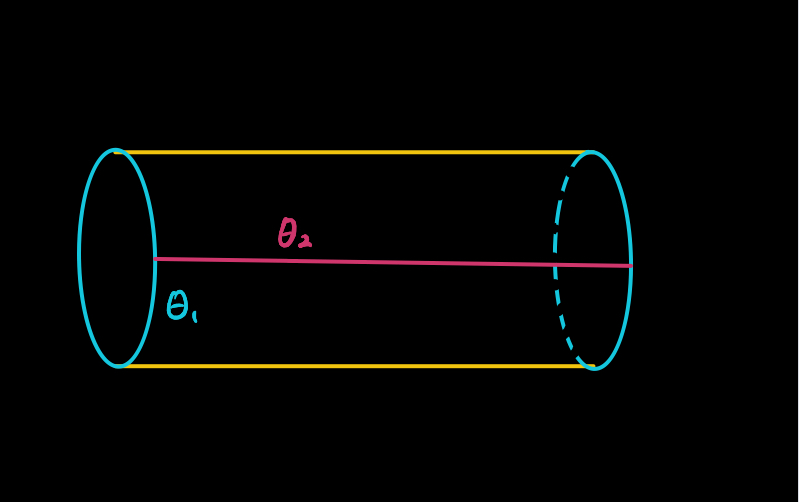
How do we specify the position of an n-uple pendulum? We can just specify the angle of each of the rods, as in the picture below. 14/n

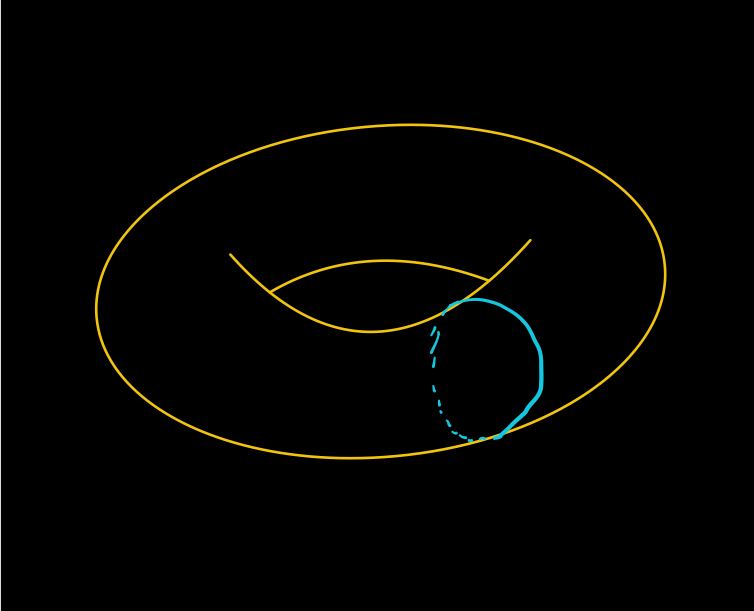
Each rod can move in a circle, so we get a product of circles, one for each rod. With two rods, this is a donut — in general, with an n-uple pendulum, you get an n-dimensional torus. 15/n

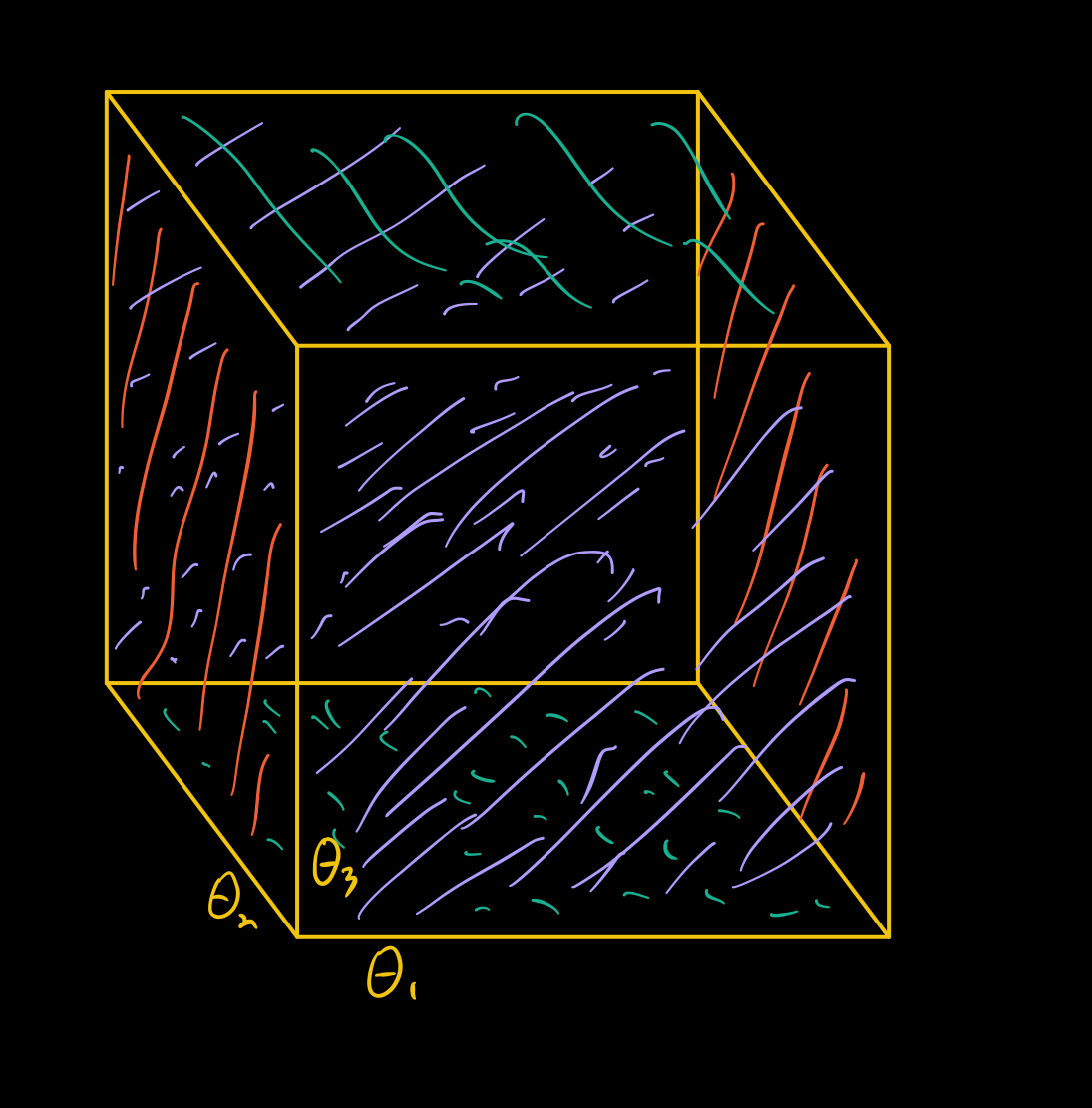
For example, when n=3, you can visualize this as a solid cube, after gluing opposite sides together (as indicated by the colors). Each axis corresponds to one of the angles. What is the topology of these shapes? 16/n

One approach to asking this question is to ask how many k-dimensional holes these n-tori have. A formalization of this is: what are the Betti numbers of the n-torus? It’s OK if you don’t know what this means. 17/n

It turns out that the k-th Betti number of an n-torus is (n choose k) — there are (n choose k) k-dimensional holes. Loosely speaking this is because you can choose any k of n possible directions, and travel around them until you return to where you started. 18/n

So there’s a numerical coincidence here — the k-th Betti number of the configuration space of an n-uple pendulum (the n-torus) is equal to the number of equilibria with k stable directions. They’re both (n choose k)! 19/n

It turns out this is in fact no coincidence. For the experts, this is because the potential energy of this physical system is a Morse function on the configuration space, and one can use Morse theory to compute the Betti numbers. 20/n

The potential function here is the sum of the sines of the angles determining the position of the pendulum, weighted by the masses of the joints. 21/n

Equilibria occur where the potential energy has vanishing partial derivatives, and the signature of the Hessian matrix tells us the number of “stable directions.” The key for us is that the Hessian matrix is non-degenerate. 22/n

For any physical system with this property — the Hessian matrix of the potential energy is non-degenerate — we’ll have a similar story. In general, the number of equilibria with k stable directions won’t *equal* the k-th Betti number, but rather it will be an upper bound. 23/n

This works for quite general physical systems — for example, it’s fun to think about this for linkages! 24/n https://twitter.com/littmath/status/1291142806807941131

What I really love about this example is how it it lets one completely visualize the critical points of the Morse function — that is, the equilibria and their properties with respect to perturbation. 25/n, n=25

By the way, I used this Desmos worksheet to make the gifs of pendulums in equilibrium: https://www.desmos.com/calculator/ndeaxiwn3x