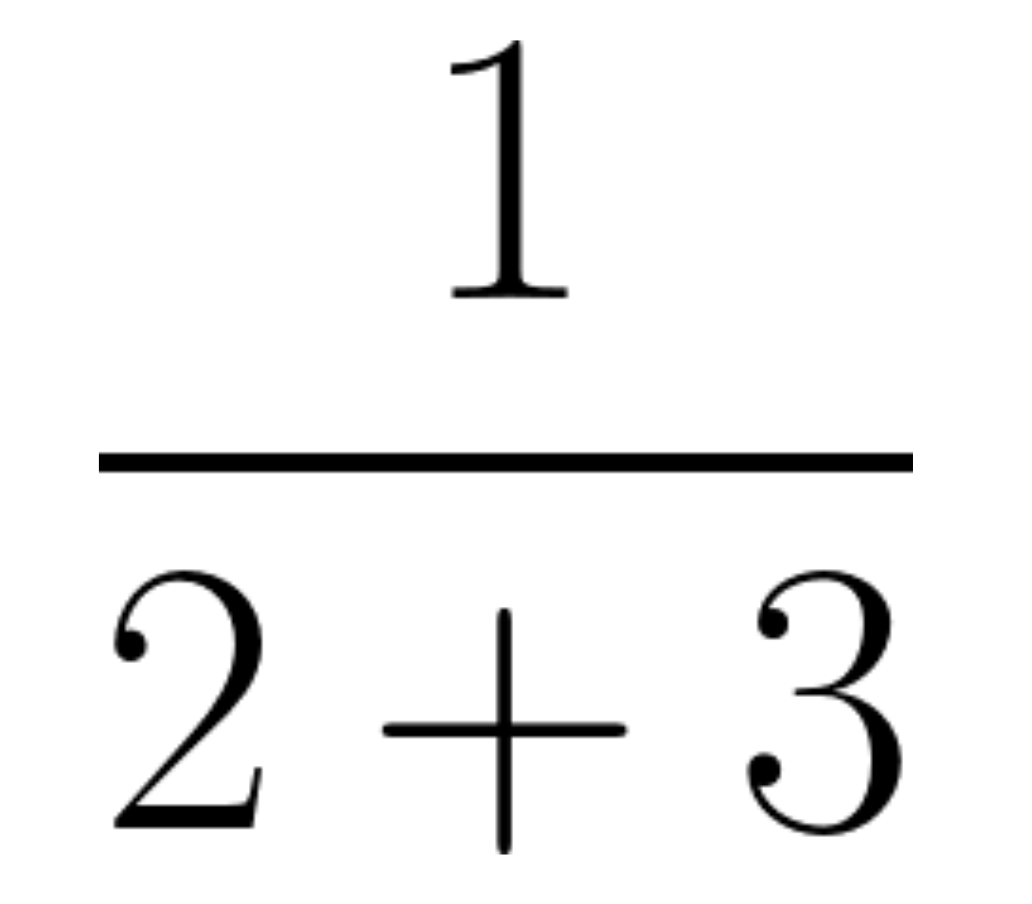Thread by @RadishHarmers, PEMDAS, my ass. Literally the only useful thing that PEMDAS/BODMAS/whatever conveys correctly [...]

PEMDAS, my ass. Literally the only useful thing that PEMDAS/BODMAS/whatever conveys correctly is that, where there would otherwise be ambiguity, notational convention is for multiplication to take precedence over addition/subtraction. A more apt mnenonic would be My ASs.

There are two other useful facts it could convey but it gets them both wrong.

One has to do with exponentiation. PEMDAS/BODMAS makes it look like exponentiation takes precedence over everything else. This is wrong. The notational convention is not for 2³ ⁺ ⁴ to be interpreted as 2³ added to 4.

The actual notational convention for exponentiation is that the base of exponentiation is the shortest expression possible (in 1 + 2³, the base of the cubing is taken as 2, not 1 + 2). The power doesn't need any such convention to parse. It's explicitly delimited as superscript.

This shortest base convention also clarifies how to read iterated exponentiation. PEMDAS/BODMAS doesn't offer any clarity on this. But in an expression like below, the base of the squaring is taken to be 3, not 4³, so the whole expression is read as 4 raised to the ninth power.

The other fact PEMDAS/BODMAS tries to convey has to do with strings of +s and -s. PEMDAS/BODMAS makes it look like addition takes precedence over subtraction.

But everyone soon learns "Actually, ignore the mnemonic, you should do addition and subtraction together left-to-right".

Even this isn't quite right, though. It's not that addition and subtraction must be done left-to-right. If you look at 3 + 4 + 5 and decide to add 4 to 5 first, and then add 3 to that, you're doing something perfectly fine.

The bother is just, in a string like -3 + 4 - 5 + 6, how far does the scope of the negation or the "thing being subtracted" go after each - symbol? Does this mean to take 3 + 4 - 5 + 6 and negate it? Does this mean to take -3 + 4 and subtract 5 + 6 from it?

The convention with a string of -s and +s is that these are punctuation separating all the values to combine. Values directly after a - are subtracted or negated, the rest are added. You can use whatever order you want, just keep track of what's subtracted/negated and what isn't.

In -3 + 4 - 5 + 6, the 3 and the 5 are subtracted, and the 4 and the 6 are added. You can combine these four values in whatever order you want. 4 minus 3, then subtract 5 from that, then add 6 onto that. Or 6 minus 5, add 4 to that, subtract 3 from that. Whatever you like.

That's it, those are the only three actual rules lumped under "order of operations".

Where there would be ambiguity otherwise:

1. Multiplication takes precedence over addition/subtraction (My ASs)

2. The base of exponentiation is the shortest thing possible.

3. +s and -s are separators, and you subtract what has a - in front of it.

What about division, you ask? Division doesn't need any of this. People normally write division vertically, one thing on top of a line on top of another thing, explicitly delimiting the numerator and denominator.

Division certainly doesn't "come before" addition, as PEMDAS/BODMAS would tell you. This doesn't mean "Divide 1 by 2, and add that to 3" or "Divide 1 by 3 and add 2 to that". But you'd never think that anyway.

When people do write division in one line with a /, all bets are off. They're not using traditional conventions and if anything looks ambiguous, you better ask them what they mean.

If someone writes 1/2π, they're more likely to mean "The reciprocal of 2π" than to mean "Half of π", but you'd really just better ask them to clarify.

It's genuinely ambiguous, just like "Bob doesn't like John because he's rude" is ambiguous as to whether it's Bob who is rude or John who is rude. Math isn't different from anything else you can say with words. It's possible to say things that aren't clear and need clarification.

And something like 1÷2π? Here's the deal. No one uses ÷ outside of elementary school. It's like writing "Congreſs". It's archaic. If you see a ÷, you're talking to someone who never actually reads or writes math. Again, all bets are off on what they mean. You'll have to ask them.

What about the very first part of PEMDAS/BOMDAS? The parentheses/brackets. Don't we need a rule to tell us that in 3 - (4 + 5), you first add the 4 to the 5 and then subtract this from the 3?

No, no one needs to tell you this, because there's no other way you could have read it. There's no such thing as adding 3 - (4 on the one hand to 5) on the other hand. 3 - (4 isn't a thing and 5) isn't a thing. You'd never have read it this way anyway.

Similarly, you'd never read 24 as meaning 2 times 4 instead of twenty-four. There's a million conventions you've internalized without anyone formalizing them for you like a dumb machine.

No one ever taught you to avoid two - symbols in a row (--6 to mean 6, or 3 - -6 to mean 3 minus negative 6), but you've internalized it all the same. You don't need a teacher to tell you hard rules for this. You learn conventions by seeing what people do, just like any language.

So that's it. Forget PEMDAS/BODMAS. Forget "order of operations". There's only three notation rules in all of it.

My ASs, shortest base, and subtract what has a minus sign in front. Just know those three.

All of this is only notational convention and has nothing to do with actual mathematical content. And the only reason it's needed is because we've picked stupid notation that doesn't make it clear where things began and end. We could've picked better notation but didn't. The end.

Eh, one last comment. If you're using a programming language, look up its rules (they vary). But human communication isn't so mechanical. If someone writes to you with this kind of spacing, you'd be an idiot to parse it as anything other than (3 + 4) x (5 + 6), PEMDAS be damned.

Latest Threads Unrolled: