My project from the @LosAlamosNatLab Summer School is finally out! We are happy to announce the...
Absence of Barren Plateau in Quantum Convolutional Neural Networks
with @MvsCerezo, @samson_wang, T. Volkoff, @sornborg and @ColesQuantum.
https://scirate.com/arxiv/2011.02966
Thread
Absence of Barren Plateau in Quantum Convolutional Neural Networks

with @MvsCerezo, @samson_wang, T. Volkoff, @sornborg and @ColesQuantum.
https://scirate.com/arxiv/2011.02966
Thread

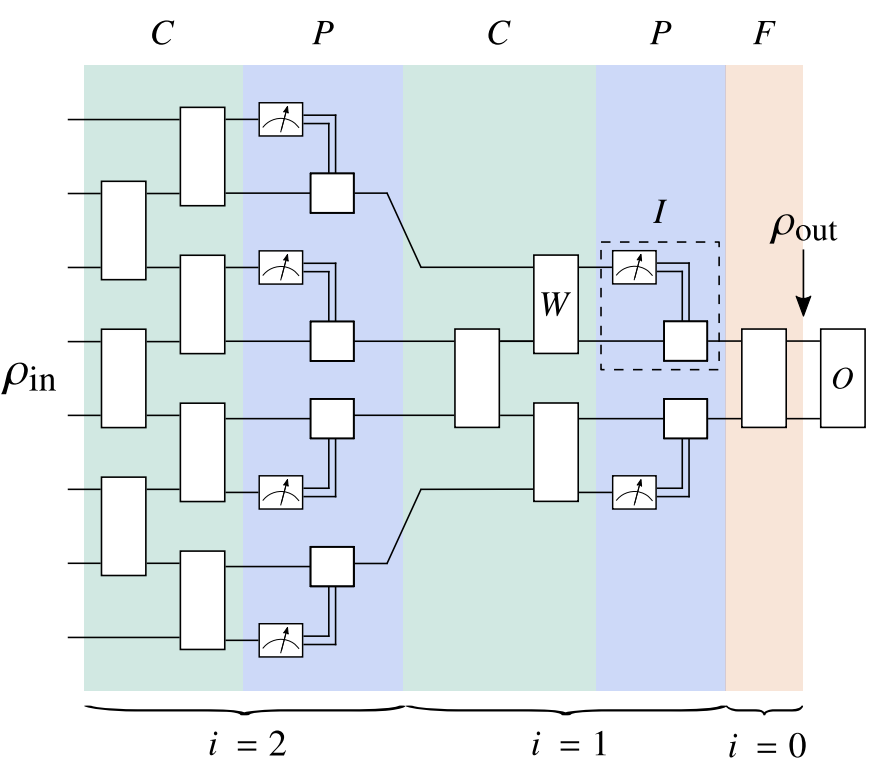
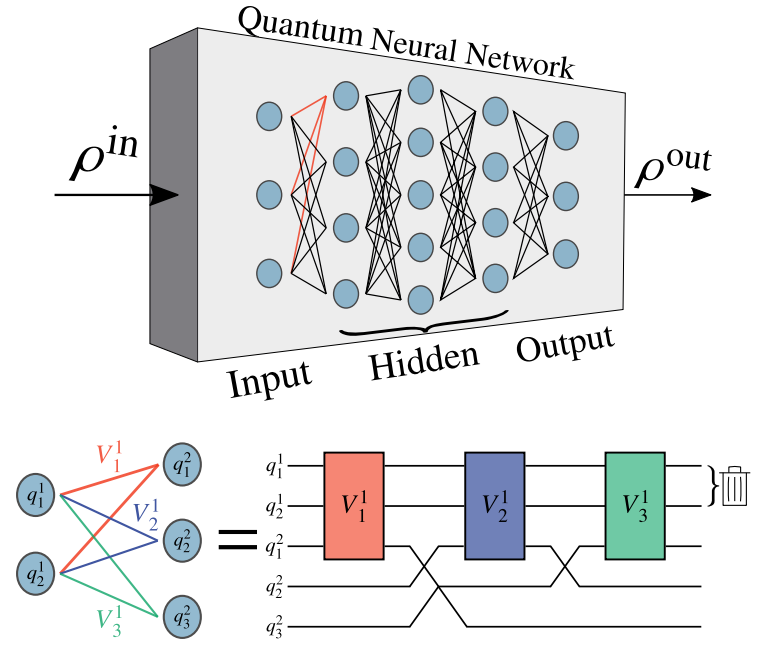
A quantum convolutional neural network (QCNN) is a type of variational circuit proposed in https://arxiv.org/abs/1810.03787 and designed for classification and regression on quantum data, e.g. determining the magnetic phase of an input state.
2/N
2/N
An important general problem with QNNs is the barren plateau (BP) phenomenon, the quantum equivalent of vanishing gradients: when a QNN is randomly initialized, its gradient tends to vanish exponentially with the # of qubits...
3/N
3/N
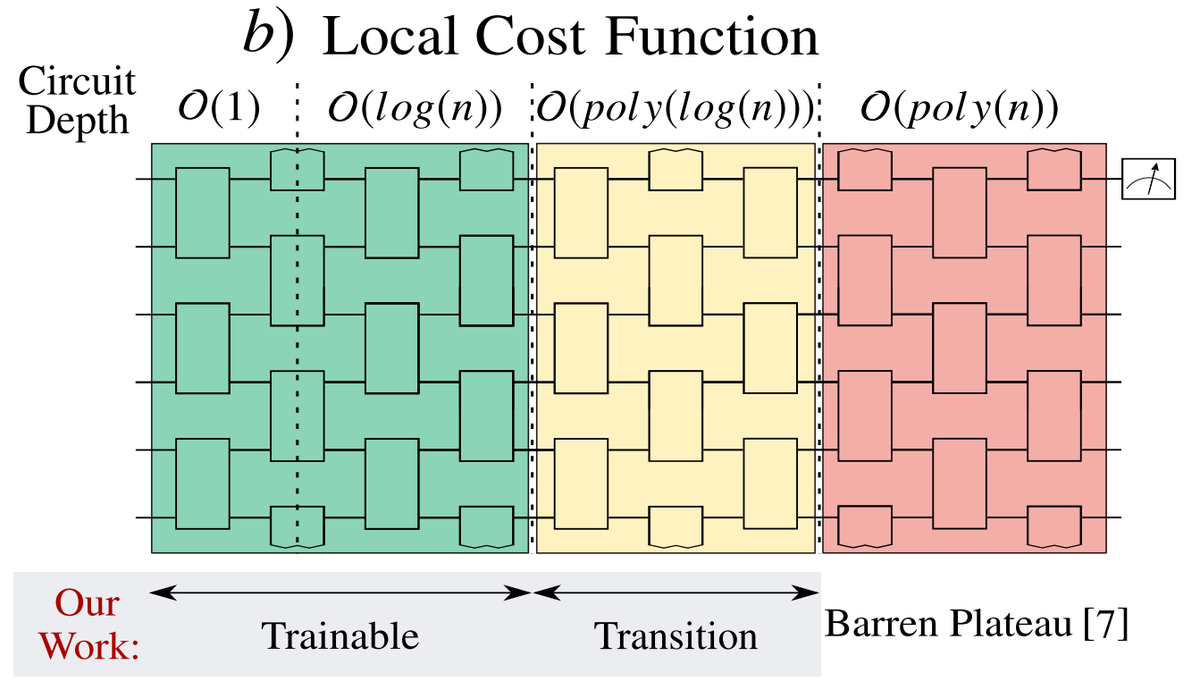
BPs have been shown to occur for many architectures, including the Hardware Efficient Ansatz ( https://arxiv.org/abs/2001.00550 ), Perceptron-based QNNs ( https://arxiv.org/abs/2005.12458 ), Quantum Boltzmann machines ( https://arxiv.org/abs/2010.15968 ), etc.
So, what makes the QCNN different?
4/N
So, what makes the QCNN different?
4/N
At each layer of the QCNN, half of the qubits are discarded (pooling layer), limiting the number of layers to log(n). And it was shown in ( https://arxiv.org/abs/2001.00550 ) that for a local cost function (as in the QCNN), the Hardware Efficient Ansatz with log(n) layers has no BP
5/N
5/N
Can we directly generalize this result to QCNNs? It's not totally obvious since QCNNs have several key differences with Hardware-Efficient Ansatzes. But using a similar proof technique along w/ some novel methods, we managed to show that the QCNN landscape is not so barren!
6/N
6/N
More precisely, we showed that the variance of the QCNN gradient is lower bounded by a term vanishing only polynomially in the number of qubits. Therefore, less than a polynomial # of measurements is needed to estimate the QCNN gradient => no BP 
7/N

7/N
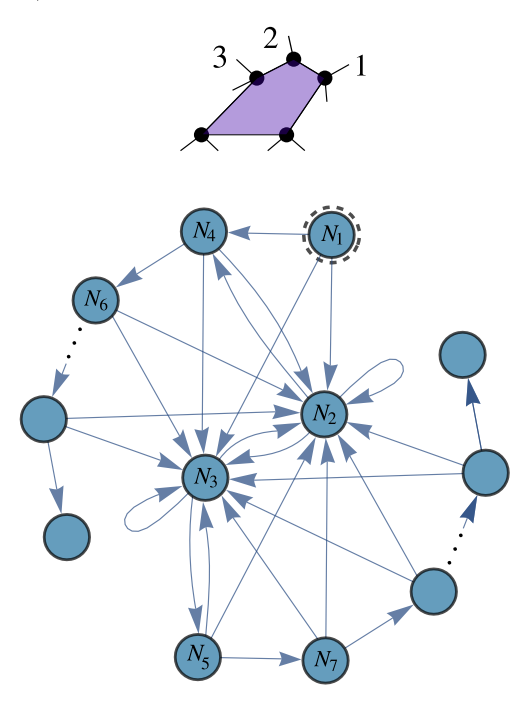
What's the main idea behind our proof? To compute the variance of the grad, we have to integrate the grad^2 when each block of the QCNN follows the Haar measure! We end up with a tensor way too big to integrate analytically! (as shown here and compared to a R&M character)
8/N
8/N
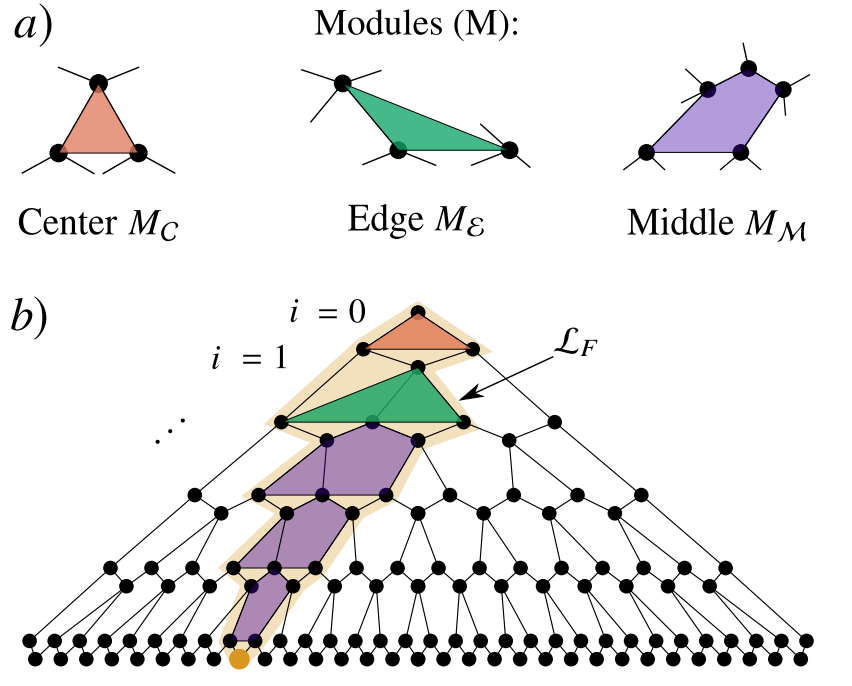
To solve this issue, we introduced a novel method, called GRIM (Graph Recursion Integration Method), where we group sets of repeating blocks in modules, integrate them sequentially, and construct a graph that keeps track of each integral (details in the paper)
9/N
9/N
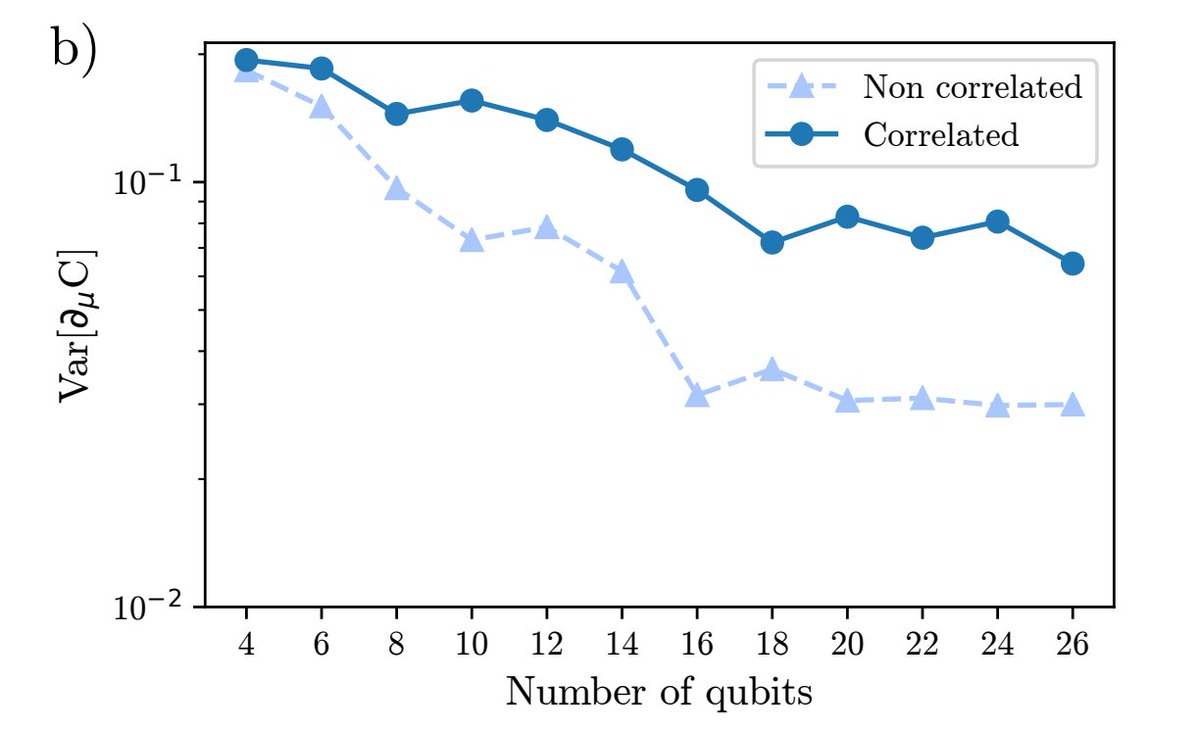
Finally, we verified our results numerically, both when the blocks share the same parameters in each layer (as proposed in the original architecture) and when they are completely uncorrelated
10/N
10/N
Spending the Summer (virtually) with all the @LosAlamosNatLab folks has been an incredible experience and I am super thankful to have been given this opportunity! It was a very collaborative project, so shout out to all the team for having made it possible! 
11/N, N=11

11/N, N=11

 Read on Twitter
Read on Twitter