Ça fait un moment que je réfléchis à faire un petit thread sur les "fits numériques" (ou "ajustements de courbe" en bon français), comment on les faits, à quoi il faut faire attention.
Donc imaginons qu'on ait des données expérimentales, et qu'on veuille "fitter la courbe".
Donc imaginons qu'on ait des données expérimentales, et qu'on veuille "fitter la courbe".
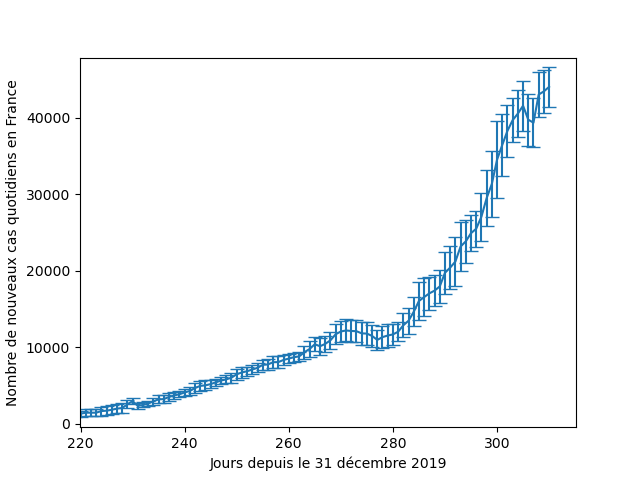
Quelques précautions avant de commencer : j'ai pris les données du nombre de cas covid comme exemple, ce qui a motivé mon choix c'est surtout : ce sont des vraies données (poke @frestagn), elles sont accessibles ( https://ourworldindata.org/coronavirus/country/france?country=~FRA), tout le monde voit de quoi on parle.
Mais (et j'insiste là-dessus), ce dont je vais parler, c'est principalement des ajustements de courbe, je ne prétends pas vraiment apporter des choses pertinentes sur l'épidémie (je ne suis pas épidémiologiste).
L'étape zéro (souvent implicite) de l'ajustement de courbe c'est qu'on a fait un choix de représentation des données : on a tracé une grandeur en fonction d'une autre, et on a donc un set de points de coordonnées (X,Y), qu'on peut tracer sur un graph en 2D.
Ce qui nous intéresse, c'est de trouver une fonction f qui "fitte les données", c'est à dire dont la courbe "ressemble" à la courbe expérimentale (au moins sur la plage de X qu'on a). Et cette fonction va en général dépendre de paramètres numériques, qu'on va chercher à estimer.
En général, il y a deux cas possibles :
- soit "on sait déjà à quoi la courbe devait ressembler" (i.e. on a un modèle qui nous dit que la courbe devrait suivre une certaine loi)
- soit "on ne sait rien" et on veut essayer de trouver une loi qui permettrait de décrire la courbe
- soit "on sait déjà à quoi la courbe devait ressembler" (i.e. on a un modèle qui nous dit que la courbe devrait suivre une certaine loi)
- soit "on ne sait rien" et on veut essayer de trouver une loi qui permettrait de décrire la courbe
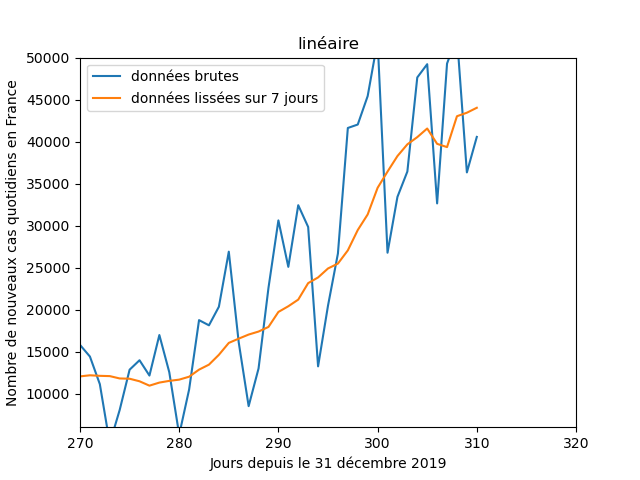
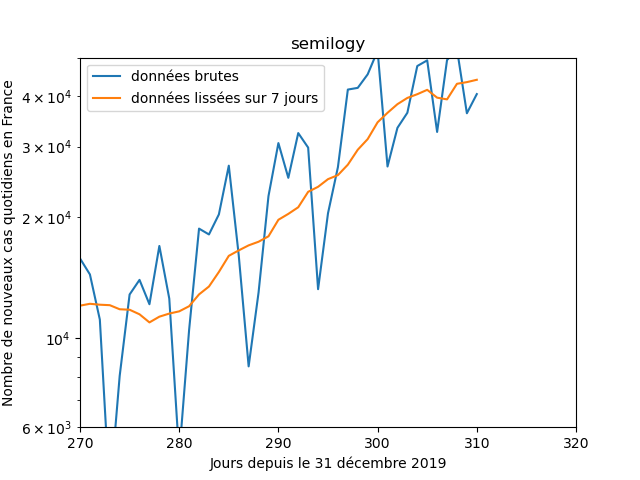
Dans tous les cas, la première chose à faire, c'est de tracer les données, pour voir à quoi ça ressemble. Ici par ex. on voit que les données sont assez bruitées (avec une baisse tous les dimanches), donc les données lissées sur 7 jours seront sans doute mieux appropriées.
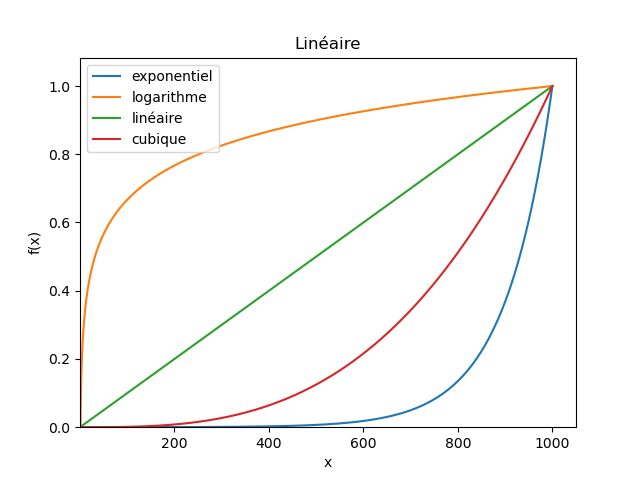
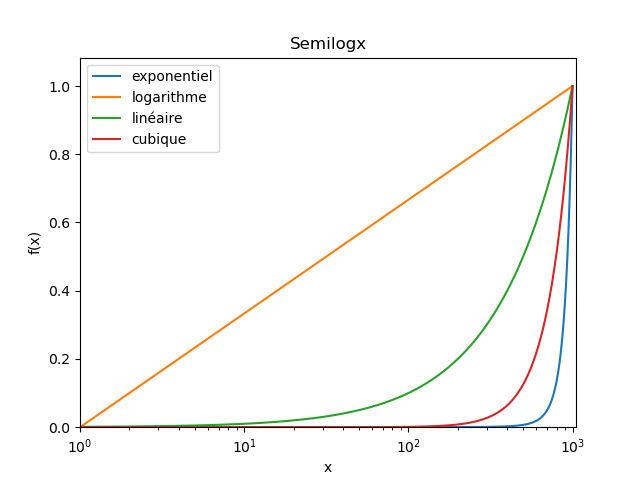
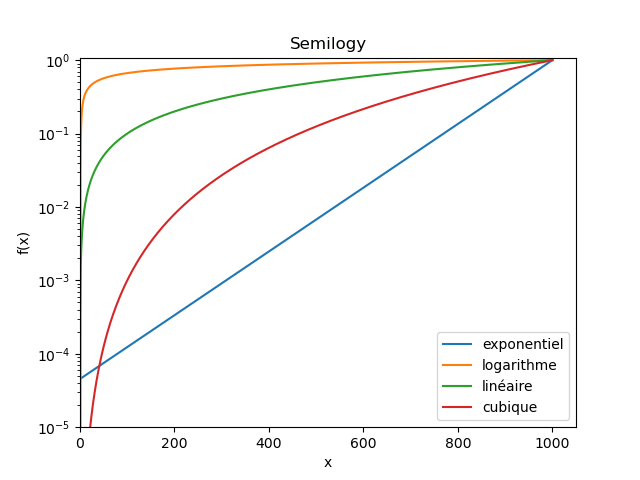
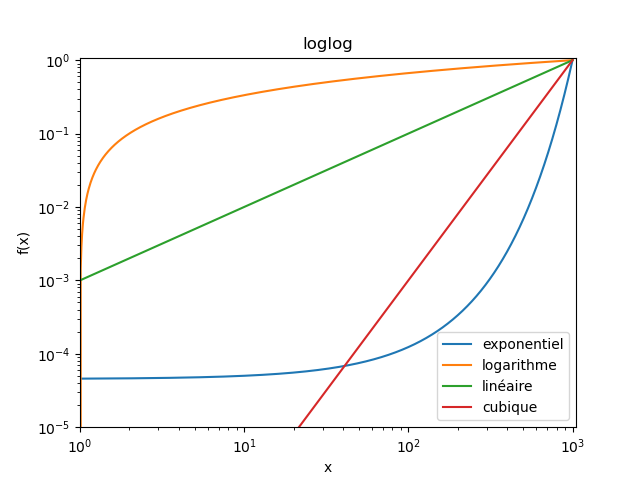
Dans le cas où "on ne sait rien", il est fréquent d'utiliser différentes représentations graphiques (linéaire, semilogx, semilogy, loglog) pour voir à quoi la courbe ressemble. L'idée sous-jacente, c'est que ces représentations permettent de "débusquer" des lois usuelles.
Par exemple ici, j'ai tracé trois lois parfaites : une exponentielle, un logarithme, une loi linéaire, et une loi cubique.
On voit que selon la représentation (linéaire, semilogx, semilogy, loglog), certaines deviennent "clairement des droites".
On voit que selon la représentation (linéaire, semilogx, semilogy, loglog), certaines deviennent "clairement des droites".
En pratique, cette technique n'est pas forcément très fiable (les différentes représentations peuvent distordre certains aspects des courbes, on peut se faire leurrer par l'échelle à laquelle on regarde les courbes, etc.), donc ça peut donner des pistes, mais c'est tout.
Par exemple, sur les données du nombre de nouveaux cas covid par jour : si je zoome sur en gros le dernier mois, ça n'est pas évident de dire laquelle des deux représentations "est la plus une droite" (les deux courbes montrent exactement la même fenêtre de temps ici)
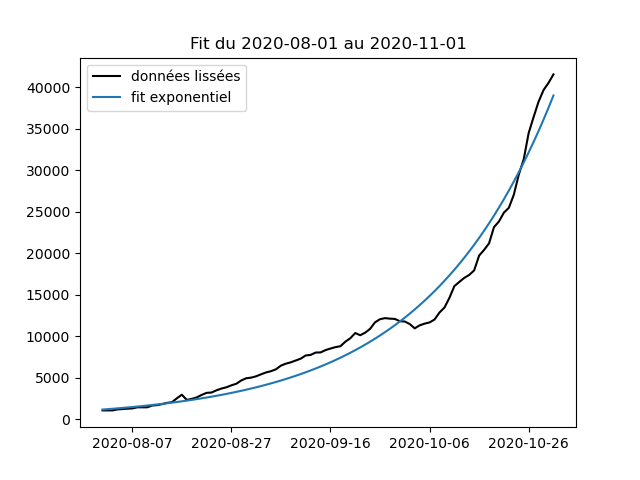
Mais ici on n'est pas dans le cas où on ne sait rien : les épidémiologistes nous disent qu'on attend plutôt une croissance exponentielle, c'est donc une fonction f telle que f(t) = A * exp(t/t0) que l'on va utiliser pour essayer de fitter les données, elle a 2 paramètres A et t0.
Juste pour que ça soit peut-être un peu plus parlant, on peut l'écrire sous la forme f(t) = B * 2^(t/t0), c'est-à-dire que la fonction part d'une valeur initiale B à t=0, et double de valeur à chaque fois que le temps t0 s'est écoulé (dans la suite j'utiliserai cette notation).
Une fois qu'on a choisi la forme de la fonction que l'on veut tester, il faut maintenant trouver les valeurs des paramètres de cette fonction qui lui permettent de coller "au mieux" aux données que l'on a (ici on veut donc trouver les valeurs de B et t0 "qui vont bien").
Sans rentrer dans les détails, il existe plusieurs méthodes, mais une qui est classique consiste à vouloir réduire l'écart entre les valeurs expérimentales Y et les valeurs f(X), et comme on veut le faire pour tous les points X, on cherche le minimum de la somme des ( f(X) -Y )²
(et comme on cherche le minimum d'une somme de carrés, c'est la méthode dite "des moindres carrés" : https://fr.wikipedia.org/wiki/M%C3%A9thode_des_moindres_carr%C3%A9s)
Là encore, sans rentrer dans les détails, il y a plusieurs sous-méthodes : dans certains cas il existe une solution analytique au problème (pour la régression linéaire par exemple), sinon on peut toujours utiliser un algorithme qui va essayer de chercher le minimum pour nous.
Juste un petit aparté : j'ai mentionné le fait qu'il existait dans certains cas des solutions analytiques (qui sont donc "exactes"), en particulier dans le cas où on cherche une fonction f linéaire (de la forme a*x+b). On peut donc se poser la question de transformer les données.
Je m'explique : si on cherche quelque chose de la forme Y = X², on sait que si on prend la racine de Y, on devrait avoir √Y = X, donc que les points (X,√Y) pourraient être fittés par une fonction linéaire. Est-ce que ça n'est pas mieux de toujours chercher à faire ça ?
La réponse c'est : "euuuuh oui et non  "
"
Dans certains domaines (par ex. à l'agrégation de physique), on ne jure que par le fit linéaire, l'idée derrière étant que "la seule chose qu'on reconnait bien à l’œil c'est une droite, donc c'est mieux pour voir si le fit est pertinent".
 "
"Dans certains domaines (par ex. à l'agrégation de physique), on ne jure que par le fit linéaire, l'idée derrière étant que "la seule chose qu'on reconnait bien à l’œil c'est une droite, donc c'est mieux pour voir si le fit est pertinent".
Sauf que : quand on fait des transformations sur les données, on fait aussi des transformations sur le bruit associé aux données (à moins d'avoir des données parfaites, mais c'est assez rare), et ça peut avoir des effets inattendus, donc ça n'est pas toujours une bonne idée...
Bref, pour l'instant, je ne vais pas faire de transformation de données, et je vais utiliser directement la fonction curve_fit de scipy.optimize ( https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html) pour trouver les meilleurs B et t0 qui permettent de fitter les données !
Et c'est là que les problèmes commencent : globalement, à moins que le modèle soit vraiment très très loin des données, l'algorithme va toujours trouver des valeurs de paramètre qui sont "les meilleurs", mais la question c'est "est-ce que les meilleurs sont bons au moins ?" 

(juste pour info, en fittant du 1er août au 1er novembre, on trouve ici B = 1557 cas initiaux, ce qui est très proche des 1155 enregistrés le 1er août, et t0 = 18 jours, c'est-à-dire qu'en moyenne sur la période, le nombre de cas aurait doublé tous les 18 jours)
La question qui se pose maintenant, c'est celle de la validité du fit qu'on a obtenu : est-ce qu'il colle bien aux données ? est-ce que c'est la meilleure fonction qui permet de décrire les données ? quelles incertitudes sur les valeurs de paramètres qu'on a trouvés ?
On a plusieurs outils pour ça, dont à ma connaissance aucun n'est parfait ("la vie c'est compliqué") mais qui permettent au moins de se faire une idée générale, et de comparer plusieurs modèles entre eux.
Le premier, c'est le coefficient de détermination :
c'est une valeur qui regarde combien est grand l'écart entre chaque Y et f(X), par rapport à combien est grand l'écart entre chaque Y et la valeur moyenne des Y, en gros plus il est proche de 1, plus "le fit est bon".
c'est une valeur qui regarde combien est grand l'écart entre chaque Y et f(X), par rapport à combien est grand l'écart entre chaque Y et la valeur moyenne des Y, en gros plus il est proche de 1, plus "le fit est bon".
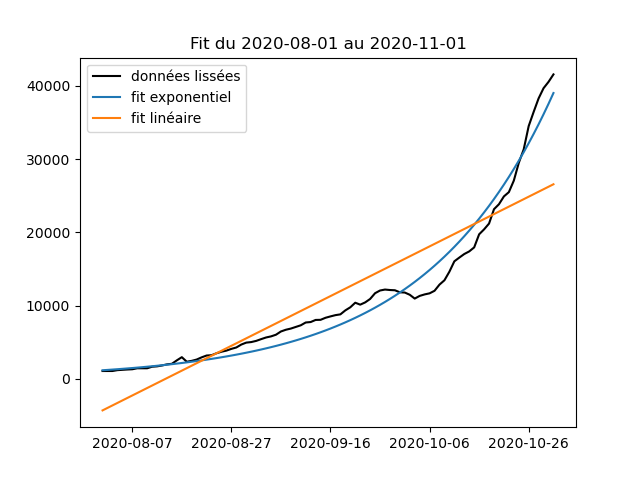
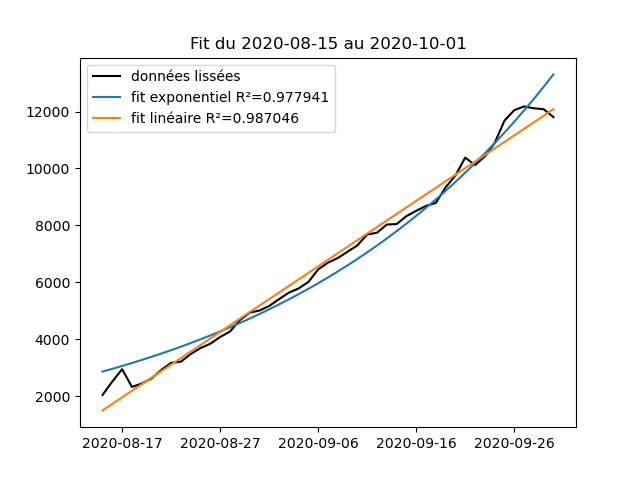
C'est donc une valeur que l'on peut utiliser a priori pour regarder entre plusieurs fits "lequel colle le mieux aux données". Par exemple ici le fit exponentiel donne R²=0,97 et le fit linéaire donne R²=0,79 (et à l'oeil on voit bien que l'un colle mieux que l'autre).
Attention quand même, une valeur proche de 1 n'est pas la garantie que le fit est bon dans l'absolu, tout ce qu'il nous dit, c'est que pour la plage de données et le modèle que l'on a choisis, on est capable de trouver des paramètres qui font que le modèle colle aux données.
En particulier, on pourrait très bien avoir un modèle "trop souple" qui s'adapte à n'importe quelles données (par ex. on peut toujours fitter N points avec un polynôme de degré N), ou on pourrait être sur une plage "trop restreinte" de données, qui ne permet pas de discriminer.
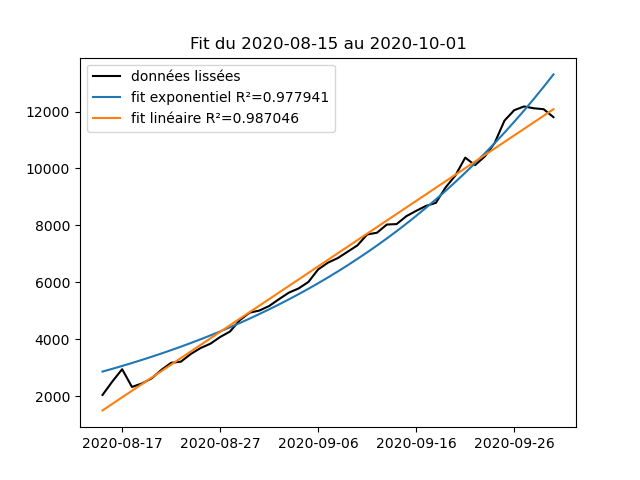
Par exemple, pour le nombre de nouveaux cas covid, si on se restreint à une plage entre le 15 août et le 1er octobre, on voit que le fit linéaire est "au moins aussi bon" que le fit exponentiel (comme l'avait fait remarquer @mixlamalice).
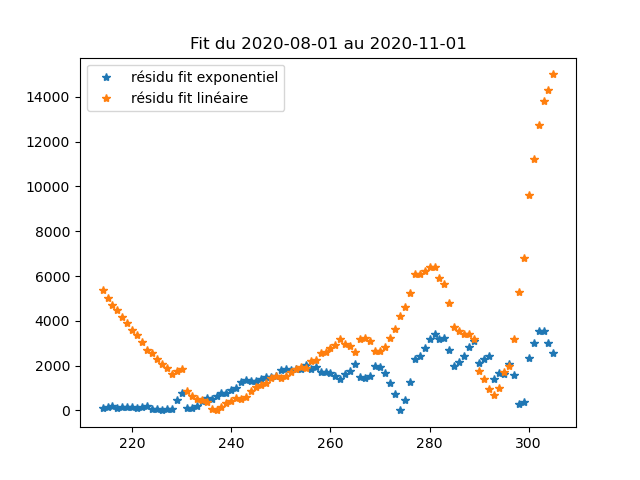
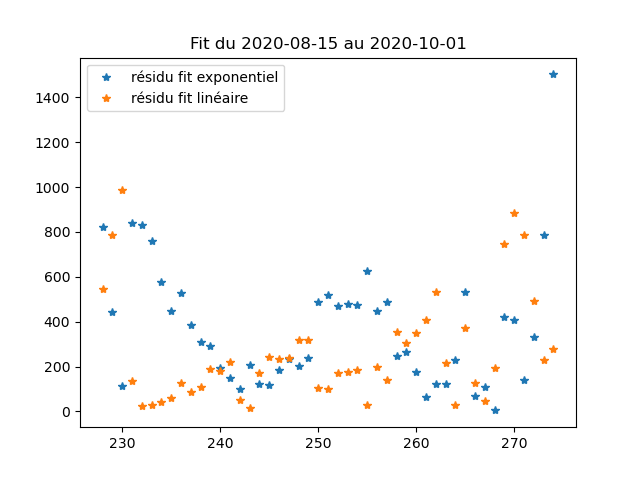
Une autre chose (qu'on ne fait pas très souvent en physique j'ai l'impression), c'est de tracer directement les résidus, c'est-à-dire les valeurs de Y-f(X) pour tous les X, et de voir si ils ont l'air "uniformes" ou si au contraire il y a des motifs qui apparaissent.
Si les résidus sont uniformes, ça veut dire que le fit est "aussi bon partout" (ce qui est bien), au contraire, si on a des motifs, ça veut dire qu'il y a des endroits de la courbe où ça colle moins bien que d'autres (donc l'accord du modèle n'est peut-être que local en fait).
(ce qu'on voit sur les données là d'ailleurs, c'est que sur la "grande plage" du 1er août au 1er novembre, aucun des deux résidus ne sont entièrement satisfaisant, mais on le voyait déjà sur les courbes : il y a des plateaux qui ne sont pris en compte par aucun des 2 modèles)
Une dernière chose qu'on peut tracer, c'est le "χ² réduit",
il est proche du R², mais ne mesure pas exactement la même chose : c'est une mesure de l'écart moyen entre les données Y et le modèle f(X), pondéré par l'incertitude que l'on a sur chaque point de mesure (σ_Y).
il est proche du R², mais ne mesure pas exactement la même chose : c'est une mesure de l'écart moyen entre les données Y et le modèle f(X), pondéré par l'incertitude que l'on a sur chaque point de mesure (σ_Y).
Et là on voit apparaître quelque chose que l'on avait caché sous le tapis pour l'instant : les points expérimentaux que l'on a peuvent avoir une incertitude associée (par exemple là on a moyenné sur 7 jours, donc on peut estimer l'incertitude comme étant l'écart type sur 7 jours)
Ce que mesure le χ² réduit c'est : compte tenu de l'incertitude qu'on a sur chaque points, est-ce que le modèle "tombe dans les barres d'erreurs ou pas" (donc est-ce que le modèle a une chance d'être compatible avec les données qu'on a).
Si χ² est grand devant 1 : le modèle est hors des barres d'erreur, donc il n'est sans doute pas adapté.
Si χ² est petit devant 1 : le modèle est dans les barres d'erreur, donc on peut dire qu'il est adapté (mais on ne sait pas si c'est le meilleur modèle pour autant).
Si χ² est petit devant 1 : le modèle est dans les barres d'erreur, donc on peut dire qu'il est adapté (mais on ne sait pas si c'est le meilleur modèle pour autant).
Deux petits points pour terminer :
En général, les fonctions qu'on utilise pour fitter peuvent toujours être approximée localement par leur développement limité (par ex. exp(x) ≈ 1 + x + x²/2 + etc.), donc si on est sur un plage restreinte, un polynôme fonctionnera toujours.
En général, les fonctions qu'on utilise pour fitter peuvent toujours être approximée localement par leur développement limité (par ex. exp(x) ≈ 1 + x + x²/2 + etc.), donc si on est sur un plage restreinte, un polynôme fonctionnera toujours.
Et enfin, est-ce qu'on peut extrapoler les données à partir du fit trouvé ?
Ça dépend : a priori même si on a un bon fit, il n'est valable que sur la plage où on a des données, si on a de bonnes raisons de croire qu'il est vrai après, on peut prolonger, mais sinon c'est risqué...
Ça dépend : a priori même si on a un bon fit, il n'est valable que sur la plage où on a des données, si on a de bonnes raisons de croire qu'il est vrai après, on peut prolonger, mais sinon c'est risqué...

 Read on Twitter
Read on Twitter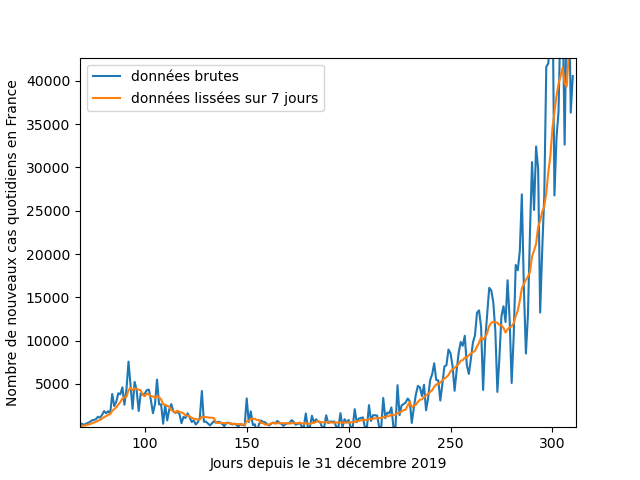
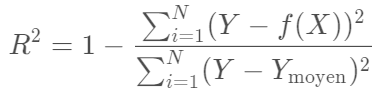
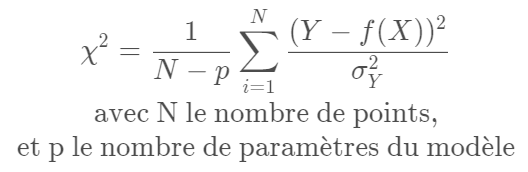
 )
)