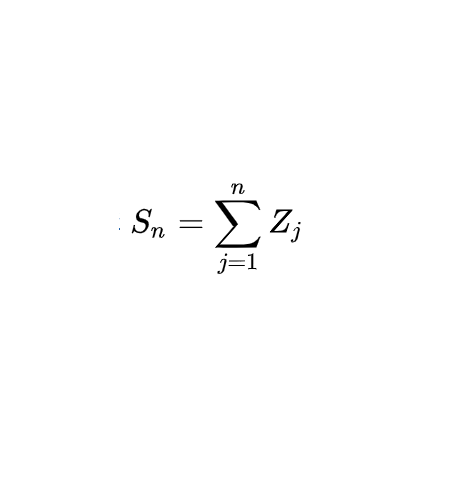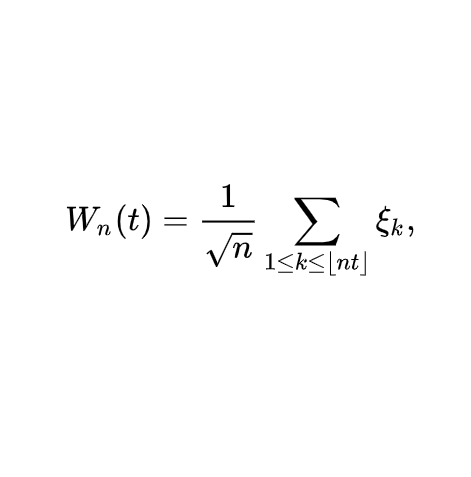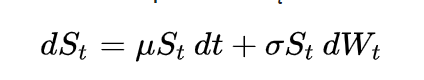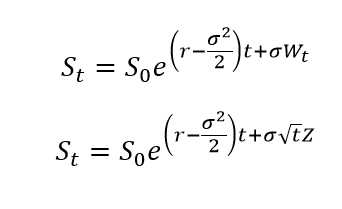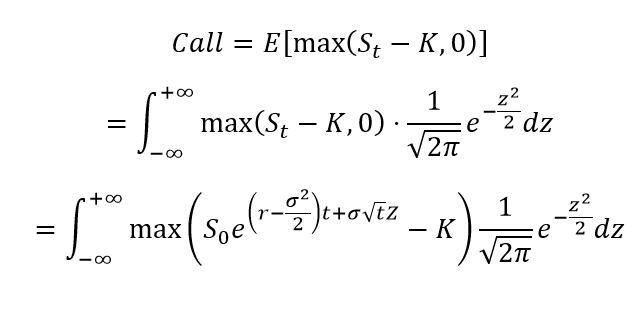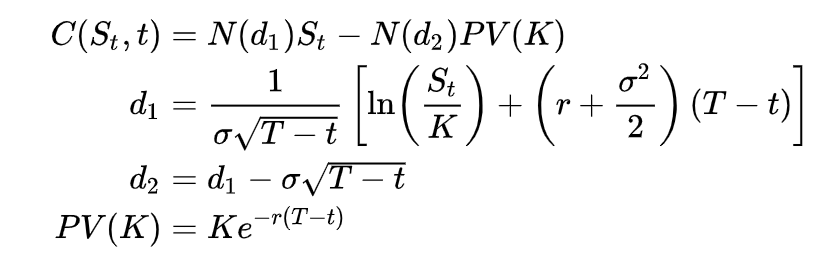I'm bored and people seem to like @bennpeifert vol explainers so here's a dollar store version of Shreve and Bjork's intro to stochastic calc for option pricing. A very rough guide to learning one way Black Scholes is derived

The simplest stochastic process is a random walk. You flip coins and either go +1 or -1.

Easy stuff

This is fun and all but how do you make this continuous? What if you flip coins *infinitely fast*? You would immediately have an unbounded process. So to make this process not go to infinity, we scale by sqrt(n) and get a Wiener process https://en.wikipedia.org/wiki/Wiener_process

There's all sorts of fun properties of this - continuous everywhere, differentiable nowhere, the distribution is normal with mean zero and variance t

How does this apply to stocks? Well stocks tend to go up over time but with some volatility.

So let's create a stochastic process driven by a Wiener process that has positive upwards drift (because stocks only go up, duh), and a random component. Geometric Brownian motion https://en.wikipedia.org/wiki/Geometric_Brownian_motion

This has the fun property that stock returns are normal while the stock price is lognormal. I'm also going to handwave stuff about Girsanov theorem and Radon-Nikodym derivatives and P/Q measure. That mu of expected stock returns magically becomes the risk free rate.

the GBM process can be solved in closed form by using Ito's Lemma on d log(St) and integrating the result. See Wikipedia or quant StackExchange for an explanation. Because Wt is just a normally distributed variable, you get a distribution that can be integrated analytically

Solving for the price of a call is just calculating the expectation of the call by integrating over Z (a standard normal variable with mean 0 variance 1). With enough change of variable and other shenanigans this can be done on pen and paper, see https://quant.stackexchange.com/questions/25711/understanding-the-solution-of-this-integral

The solution to this integral is the good ole Black Scholes formula. It's literally high school calculus https://en.wikipedia.org/wiki/Black%E2%80%93Scholes_model#Black%E2%80%93Scholes_formula

I handwaved through a lot of stochastic calculus but barring those bits, it's fairly simple freshman continuous probability distributions and calculating expectations by integral.

There are other derivations but this one has always been the easiest. One derivation is 'what if I hold a call and want the value of my portfolio to always be perfectly delta-hedged' but I always found this explanation harder.

The Kolmogorov backwards equation is also used to turn geometric Brownian motion into the Black Scholes partial differential equation https://en.wikipedia.org/wiki/Kolmogorov_backward_equations_(diffusion)

The inverse of this is using Feynman-Kac to turn the Black Scholes PDE into a stochastic differential equation https://en.wikipedia.org/wiki/Feynman%E2%80%93Kac_formula

This is why I tell people you can sound really smart saying this - you can solve option pricing in PDE-land using Crank-Nicholson or Runge-Kutta, where everything is deterministic, or in SDE-land using Monte Carlo.

The ability to go between PDE and SDE is because of the properties of Kolmogorov backwards eqn and Feynman-Kac. It's really neat and elegant.