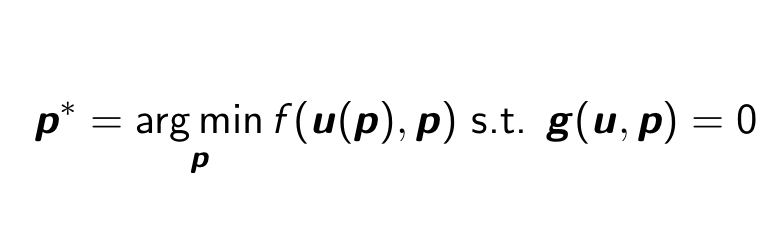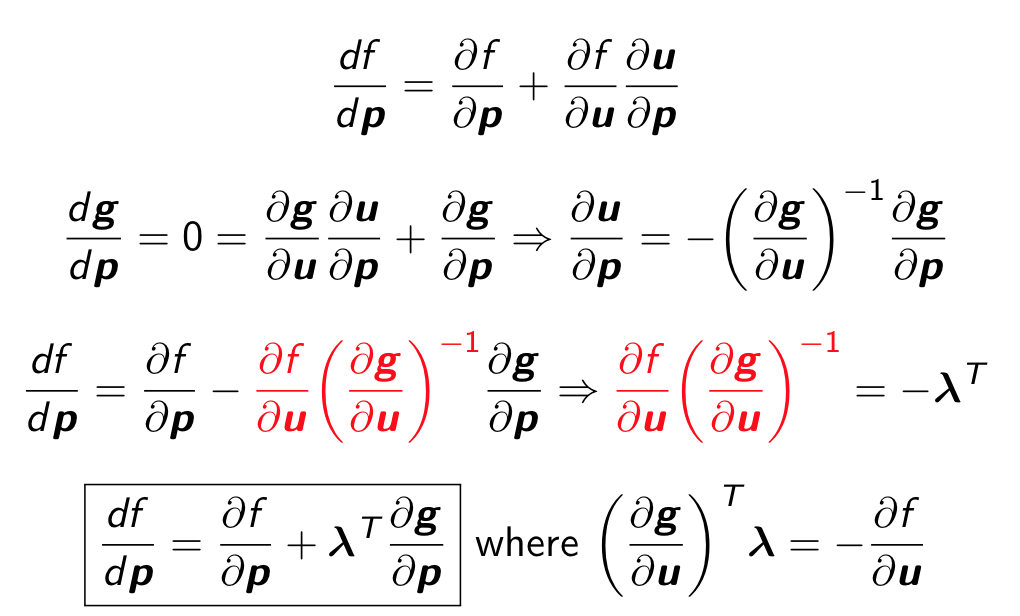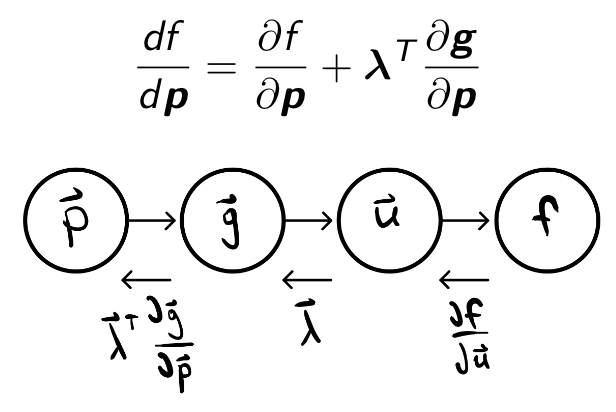The adjoint method for PDE-constrained optimization: the conclusions of my 9-month struggle to understand the word "adjoint".
I'll be talking about how automatic differentiation (AD) can help us better understand the adjoint method, and vice versa. Let's get started!
1/
I'll be talking about how automatic differentiation (AD) can help us better understand the adjoint method, and vice versa. Let's get started!
1/
PDE-constrained optimization is often formulated as shown here. The goal is to use gradient-based optimization to minimize an objective function, f. The problem is that f depends implicitly on the solution u to a system of possibly non-linear equations, g=0. Oh no!
2/
2/
It turns out we can differentiate that implicit function by making use of the chain rule. It turns out that to do so, we solve an adjoint equation (a linear system, in this case) for an adjoint vector λ, which we use in our formula for the derivative.
3/
3/
But that brings up so many questions: what even is an adjoint equation? And what is an adjoint vector? And is the adjoint method related to automatic differentiation (AD)? If so, how?
To get to the bottom of this, let's briefly take a high-level look at AD.
4/
To get to the bottom of this, let's briefly take a high-level look at AD.
4/
AD is fundamentally (1) "primitive operations" and (2) compositions of Jacobians. Primitive operations are the building blocks of functions computed by an AD tool. These could be simple primitives like sin, exp, div or high-level primitives like matmul, fft, odeint, etc.
5/
5/
For each primitive operation, AD tools know how to compose the Jacobian of that primitive operation with other Jacobians to compute the full Jacobian. In forward mode, we compose Jacobians from beginning to end, and in reverse mode we compose Jacobians from end to beginning.
6/
6/
Actually, this is often too slow, so we stick a vector at the beginning and compute Jacobian-vector products (JVPs, forward) or at the end and compute vector-Jacobian products (VJPs, reverse).
In optimization of a scalar f, we use the vector [1.0] at the end to compute VJPs.
7/
In optimization of a scalar f, we use the vector [1.0] at the end to compute VJPs.
7/
Does the adjoint method fit into our AD framework of (i) primitive operations and (ii) Jacobian products? Yes!
g=0 can be understood as a primitive operation taking p and outputting u. The adjoint method, then, is just how we compute the VJP of the primitive g=0!
8/
g=0 can be understood as a primitive operation taking p and outputting u. The adjoint method, then, is just how we compute the VJP of the primitive g=0!
8/
To expand a bit more:
df/du is the "V" in the VJP. λ is the result of the VJP. The linear system for λ, the "adjoint equation", is the equation whose solution gives the VJP of the primitive g=0.
Hopefully this is a simpler way of understanding the adjoint method!
9/
df/du is the "V" in the VJP. λ is the result of the VJP. The linear system for λ, the "adjoint equation", is the equation whose solution gives the VJP of the primitive g=0.
Hopefully this is a simpler way of understanding the adjoint method!
9/
Framing it in this way allows us to define our terms.
An adjoint equation is an equation that computes the VJP for a given primitive operation. E.g., the adjoint equation for y = sin(x) is dx = cos(x) * dy. No linear system in this adjoint equation, just a multiply.
10/
An adjoint equation is an equation that computes the VJP for a given primitive operation. E.g., the adjoint equation for y = sin(x) is dx = cos(x) * dy. No linear system in this adjoint equation, just a multiply.
10/
The adjoint vector is the vector that gets passed into a VJP. Since these VJPs are being composed, an adjoint vector is both the input & the output of a VJP.
I prefer "cotangent vector" (thx to @SingularMattrix). This is consistent w/ "tangent vector" & is less confusing.
11/
I prefer "cotangent vector" (thx to @SingularMattrix). This is consistent w/ "tangent vector" & is less confusing.
11/
So AD helps us better understand the adjoint method. But what about vice versa?
Thinking in terms of adjoint equations gives us a different perspective on rev. mode AD: rev. mode AD libraries know how to setup & solve adjoint equations for each primitive in the library.
12/
Thinking in terms of adjoint equations gives us a different perspective on rev. mode AD: rev. mode AD libraries know how to setup & solve adjoint equations for each primitive in the library.
12/
Thinking about AD in this way helps us understand how it might eventually fit into the broader field of computational science: one could imagine implementing composable adjoint eqs. for methods used across computational science. (MPI? Grid generation? PETSc? Etc.)
13/
13/
Particularly inspiring is the dolfin-adjoint library, which treats the entire FEM solution to a PDE as a primitive operation, then derives the adjoint equations automatically.
Thanks for reading! Thoughts?
14/14
Thanks for reading! Thoughts?
14/14

 Read on Twitter
Read on Twitter