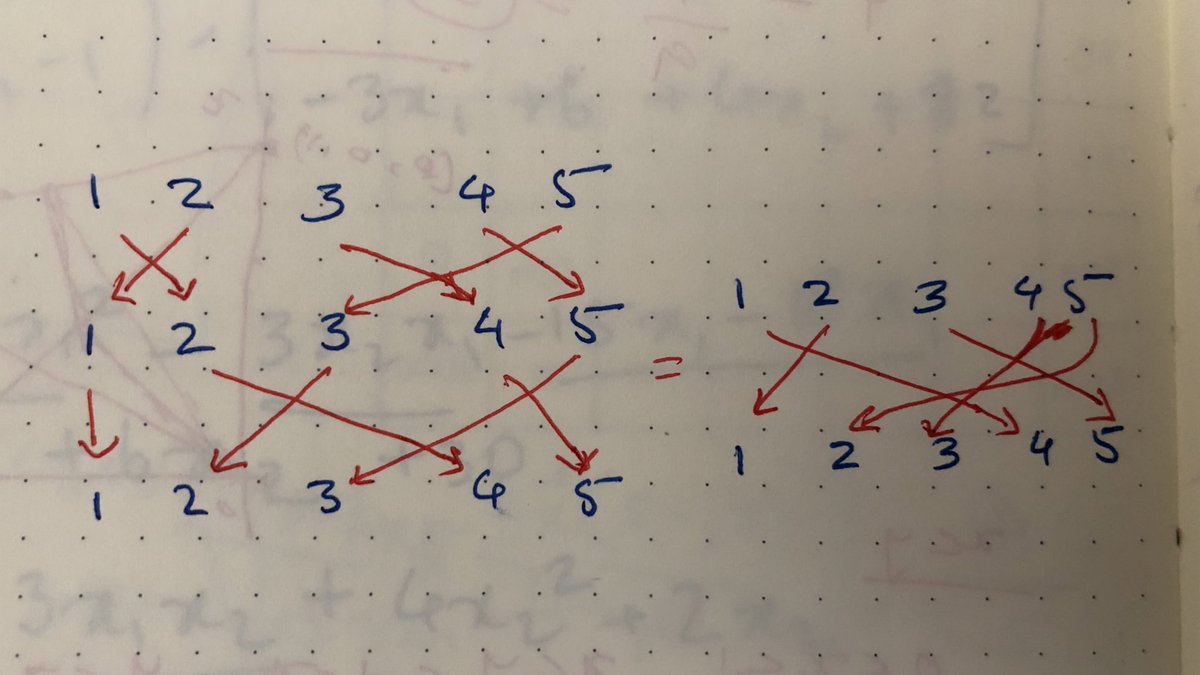I want to post maths. Would you like to hear about symmetries, permutation groups, and why six is a magic number?

Okay, I'm not sure how far into this I can get, but let me try.
I want to try and convey what motivates me to think about the problems I like to think about, things I find beautiful and why I find them so.

Let's start with a very basic type of mathematical object, shapes in the plane with more than two sides, where a "side" is a straight line segment. Your triangles, quadrilaterals, pentagons, hexagons, heptagons, octagons and the like. Mathematicians call these polygons.

Now there are many kinds of mathematics and many kinds of mathematician, so different mathematicians use these shapes as jumping of points for different investigations. Some, the ancient Greeks, e.g., care about the lengths of sides and angles and what you can say about those.

More recently, many have pondered how we can play around with the idea that these shapes are in the plane. What if we looked at shapes like this on spheres and other spaces? What does "straight line segment" mean in these contexts? This has also led to very rich fields of study.

Some people, my people, prefer other aspects of studying shapes, we like particular shapes for their symmetries, and try and understand what symmetry means, and what contexts we can apply them to. We like that symmetry is inherent to objects and their relations.

So to study symmetry, we strip off many aspects of what we see when we look at shapes, and look at just what interests us. It's a common theme in how mathematics is done: keep the stuff that interests you, drop the rest, see what you get, see how far you can push it.

So if we are going to look at polygons, we look at "regular" polygons. We decide all the sides of our polygons have the same length. So the triangles we care about are equilateral triangles.

If we also decide that we only care about shapes where all angles between sides are also equal, the only kind of quadrilateral we care about is a square. Then we have regular pentagons, regular hexagons etc.

Now, what is "nice" about these particular shapes? Symmetry!

Most people find symmetric shapes more pleasing to their eyes and minds. And the forces of physics that shape our natural world too end up creating symmetry all around us, from crystals to viruses.

Now, as mathematicians, what we want to do is dig deeper into the concept of symmetry. What is it? Is there more than one kind? Which ones are interesting? Are there more than you see every day in nature, ones you can't just draw on paper?

So what is it? One way of ascribing symmetry to an object, which we have decided to agree on, is that it remains unchanged under certain transformations.

Take an equilateral triangle, as three beads connected with rigid wires of equal length, if you like. Rotate it around, flip it along some axis going through one vertex and the midpoint of its opposite edge. It still looks the same.

Unless you can tell the original vertices (corners) of your triangles apart, you can't tell if the vertices and edges (sides) have changed places.
Now it's useful to quantify the rotations and flips that don't change the essential "equilateral triangliness" of our triangle.

In order to do this, let us colour, or equivalently (and because I can't be bothered to do a graphic now) name, our vertices, so we can keep track of them even if we only still care about their being vertices of an equilateral triangle.

Note that once we name the vertices, we don't need to give edges new names, we can identify each edge in terms of the vertices that it joins, so here the edges are AB, AC, and BC.

So that's that set up, so we can start looking at the transformations that let us move the triangle around while maintaining its shape, and position in the plane. The new point D is right in the centre of the triangle, it is equidistant from all vertices and edges.

Each line from a vertex through D bisects the opposite side.
We can flip the triangle about each of these three lines, so one vertex stays the same, the other two change places.
We can also rotate the triangle about D ,120 degrees, and 240 degrees, clockwise and anticlockwise.

(The edges and interior points, if you care about those, are also transformed, but their fates are determined by what happens to the vertices. Looking at these tells us nothing new, tracking the vertices gives us all the information you want.)

Are there other transformations? Let's leave that question aside for a moment and think about how many transformations we already have.
There are three flips. One fixes A in place and swaps B and C, another fixes B and swaps A and C and the third fixes C and swaps A and B.

How about rotations? There's one 120 degree clockwise rotation, and one 240 degree clockwise rotation, but these are, (in reverse order,) just the rotations we get if we try rotating the triangle anti-clockwise instead.
It's okay to take a moment to get your head around this.

What about the 360 degree rotation or "non-rotation"? This essentially plays the role of zero in arithmetic. It's a useful thing to have. If you apply a rotation three times, or apply any of the flips twice, you are back where you started, so it's more useful to have a zero here.

Now there's nothing special about the initial configuration of vertices we started with. Any one of the six configurations, the original one, and those obtained from its two rotations and three flips would have done equally well. The transformations are what we're interested in.

Are there more transformations? Remember, we are only interested in transformations that send one vertex to the position originally occupied by a vertex.

So the vertex A, after a transformation, can occupy the original position occupied by A, B or C. Which leaves two positions for B to occupy, and this determines C's position.

So if we think purely in terms of rearranging vertices, and why not, there are six rearrangements of vertices allowed under our rules.

Now how about if we try and apply more than one transformation? Try two flips in succession, or two rotations, or flip and rotate, or rotate and flip, then look a the results?

This seems like a good place to give our transformations names, so I don't have to type out "rotation" over and over.
Let's denote the flip fixing A by FA, similarly with B and C. And let's call the non transformation O for zero, then R120 and R240 for those clockwise rotations.

So our transformations are O, FA, FB, FC, R120 and R240. We are going to do what we call a composition. Start with a triangle (picture it with top vertex A, B bottom left, C bottom right) apply, say FA, then FB. Then see where the vertices land.

Applying FA, swaps B and C, so B is now bottom right and C is bottom left. Now what does it mean to apply FB? Do we think of B as occupying its original position? Or do we start anew, B is where it is now. Both are fine, really, but we need to pick one and stick with it.

Let's go the "memoryless" route, where FB means we fix B, wherever it is, then swap A and C, wherever they are. So what do we get?
B remains on the bottom right, C is on top, A is on the bottom left. Is this a new transformation? Is it one of the original ones?

Well, best way to find out is to draw a picture. And who do we have here? It’s our old friend, the 240 degree clockwise rotation!

Note that the order in which we apply these transformations matters to the outcome. If we applied FB and then FA to the original triangle, we get R120. (But you wouldn’t get FC, isn’t that interesting!)

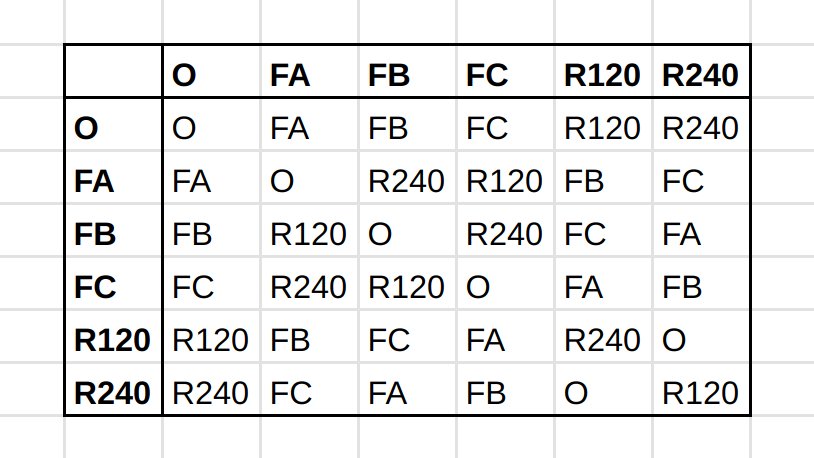
So a cool thing to do, which you can learn a lot from, depending on how long you want to stare at it and notice things, is to write down a table of compositions for all 6*6=36 pairs of transformations we have. Try it!

Here's one I made (here we apply left, then top). See how whichever transformations you compose however, you end up with one of the six you started with? Also, notice how each row and column is a rearrangement of the six with no repetitions? What other properties can you notice?

And if you worked it out yourself, congratulations, you constructed your very first group!

Now before I go on, I've been trying write this for people with no higher mathematical education. Not sure how well I'm managing to do this. So please let me know if you've followed this far, or where I lost you if I did. And do ask questions wherever you have them. Thanks!

Okay, so we said that what we constructed, this table telling you how to combine transformations, is a group.
So what is a group, in mathematics? I am not going to tell you, you can find definitions on the internet or in books. I want to tell you how how to think about groups.

For the purposes of this conversation, a group is a collection of transformations of some object that preserve the object. In our example so far, the object is a triangle, or its three vertices, when you come down to it.

These are the things to keep in mind:

There is a zero-transformation.

Any two transformations can be combined to get a transformation also in the group, and the rules for combining them give you a table like the one above.

Every transformation has an reverse or inverse transformation.

There are other properties, which we will identify and state are we meet need them.

What I really want you to take away is that a group of transformations of an object is a self contained universe in itself, describing all the transformations that you decide are allowed.

For example you could decide that all transformations of the triangle "have to stay on the plane throughout", which would mean no flips are allowed, you would end up with the group containing only the three rotations O, R120 and R240. This too has all the properties of a group.

So we have constructed a group, all transformations of a triangle that send vertices to other vertices (which we call symmetries), and a "subgroup" containing just the rotations. How shall we proceed?

One option is to look at other shapes, and do the same with their symmetries.

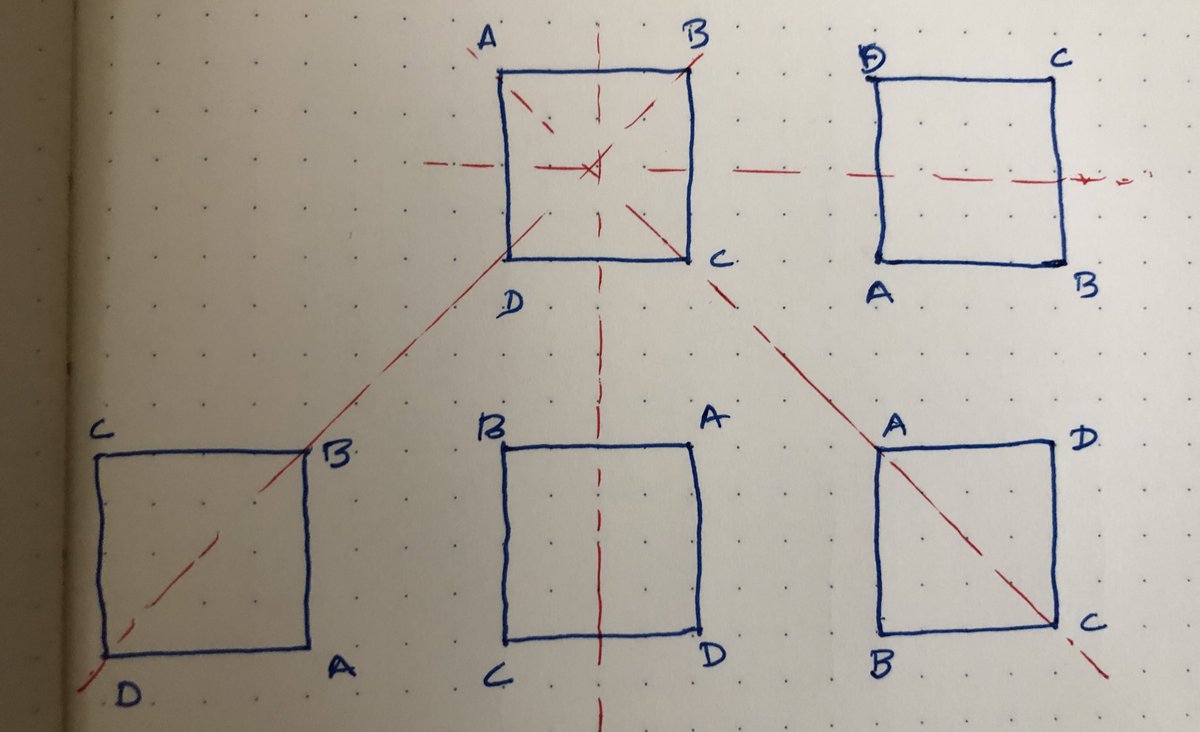
So moving on to the next regular shape, let's look at the square. How many symmetries does it have? It takes some working out, so I recommend taking out pen and paper and drawing some flips and rotations.

Mathematics is not a spectator sport, as I often tell my students.

I must go to bed now, but I’ll pick this up tomorrow. Until then!

I had stuff to do yesterday, (and I'm glad I didn't scab on #ShutDownSTEM in this one way at least) but I'm back now and ready to talk groooooups!!
I also took some time to try and learn how to animate transformations, but I am stuck, for now.

I want to make cool things like this. I feel like animations and interactive visualizations can go a long way towards making the hands-on fun of maths more accessible to many more people than it currently is. https://twitter.com/jenuflexion/status/1270473936250253314?s=20

But for now, sticking with old pen and paper, let's look at those symmetries of the square.

Did you find eight?

Four rotations...

... and four reflections?

And how do we know there aren’t more? Can we use a similar argument to the one we used for the triangle to show that there are only eight possible transformations of the square? https://twitter.com/yet_so_far/status/1270387515321655303?s=21 https://twitter.com/yet_so_far/status/1270387515321655303

Remember that we are only allowing transformations whose result also look like squares. So no twists or tears! Proceeding as before, the vertex A has to occupy one of four positions. This fixes the position of C which is diagonally opposite to A, and leaves two choices for B & D.

So we have the group of all transformations of the square, which has size (technical term: order!) eight, and it’s a good exercise to write down the table of their compositions.

Now there is no reason to stop at the square. We can play this game with every regular polygon. You get a new group in each case, whose order is twice the number of your polygon’s sides. (Why?)
So in theory, we have constructed infinitely many groups!

The groups in this infinite family of groups that we have constructed are called Dihedral Groups. And each of these has a subgroup of order the number of sides of the corresponding regular polygon, consisting only of the rotations, and we call that the Cyclic Group of order n.

So that’s two infinite families!

Now, where do we go from here?

Can we make more groups? Or to be more precise, can we take any object geometric or otherwise, identify the transformations that preserve the shape (or more broadly, structure) of that object, and see if the set of all those transformations, and their compositions, form a group?

I see absolutely no reason why not, Do you?

For a start, how about higher dimensional shapes that are like regular polygons in some way? Or irregular polygons?

Draw an isoceles triangle, (two congruent sides, one different) or a scalene triangle (three unequal sides), and try and identify its symmetries.

If I say that the more symmetries you have, the more symmetric your object is, would you agree?

But let's take a quick look at some symmetric higher dimensional shapes and their symmetries. How many such shapes can you think of? In three dimensions, to start with?

Well, I immediately think of the platonic solids, and if you're not familiar with them, here's a nice video from @numberphile where they tell you all about all of them.

Again, these are very beautiful objects which have inspired different mathematicians (and non-mathematicians!), in various ways, over millennia. I want to look at their symmetries.

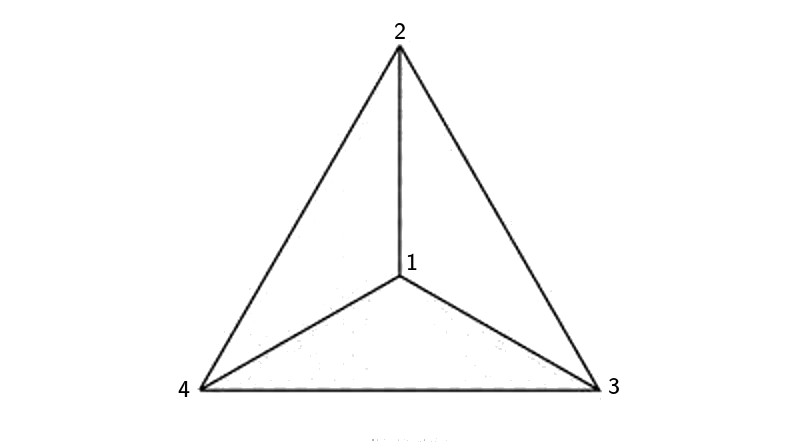
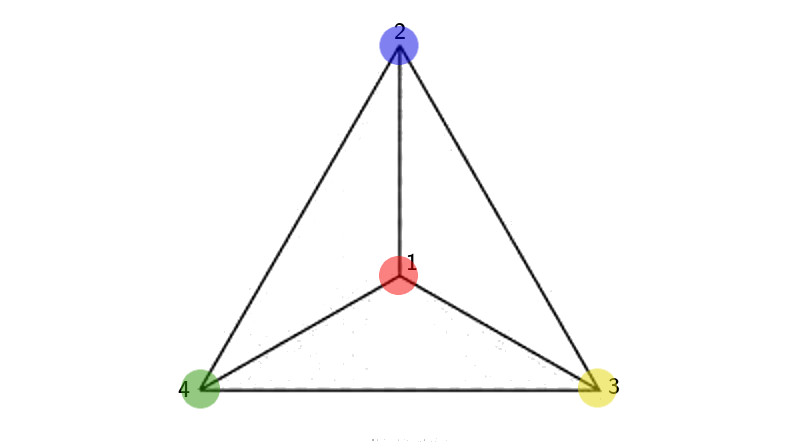
Let’s start with the smol bean, the tetrahedron. Just four vertices, six edges and four triangular faces. How many symmetries can there be?
(I think the gif is by @johncarlosbaez, btw)

Well, first let’s make clear an explicit what counts a symmetry here, because reasonable people can disagree on this.
Remember when we talked about flips of planar polygons? We had a mental picture of taking a wire frame or cardboard cutout model and flipping it over.

But I want you to think for a moment about what this fairly non-controversial transformation physically entails. Can you flip your polygon model without lifting it off the page/table/whatever surface it is on?
Or, if you could only go backwards or forwards how do you turn around?

Since we experience a mostly three-dimensional physical reality. Flipping a two dimensional object by rotating it through three-dimensional space is something we do without thinking. But what if our object itself is three-dimensional? Can we allow rotations in a fourth dimension?

To me, the answer depends on what we are looking to do with the answer. Is it a physics problem asking about possible outcomes of physical operations? Is it solely a mathematical problem, in which case...

So let us try both approaches.

CASE 1: In which we respect physical reality.

CASE 2: I spit on your physical reality.

Case 1: Does the requirement that the transformations be physically achievable with a solid tetrahedron actually rule out any potential transformations? Say, for a moment, you think of all potential rearrangements of vertex labels as potential transformations.

For one, we can’t just swap two vertices and leave the other two in place.

What else is impossible? It’s worth taking a bit of time to ponder this over.

And what is possible? We can fix one vertex in place and rotate the opposite face, giving four choices of fixed vertex times two non-zero rotations, for a total of 8 transformations. These are rotations around an axis joining one vertex and the midpoint of the triangle opposite.

You can leave everything in place, that’s our identity or zero element.
And what else? Well, look at the tetrahedron again. Every edge of the tetrahedron has an opposite edge, forming a pair of what we call skew lines. They are sort of perpendicular, but also on different planes.

What if I draw an axis joining the midpoint of one edge and the midpoint of the opposite edge, and rotate the tetrahedron 180 degrees around this axis? That’s a transformation too, it swaps pairs of vertices! Can you picture it? Here’s an image I lifted off math.stackexchange.

And how many of these double swaps are there? We have one for each pair of opposing vertices, which gives three in total. (A good way to see this is to colour opposing edge pairs the same.)

So we have identified twelve transformations, in the realm on the physically possible.

Are there more? Let’s leave that question aside for the moment and look at the transformations that are not necessarily physically possible, what we called CASE 2 earlier.

But I didn’t sleep last night and I’m tired, so I’m going to catch up on my and come back tomorrow.

Right, I'm back and ready to go on. How are we to think about transformations that are not achievable by rotation?

It's hard to imagine transformations in four-dimensions and beyond. For me, personally, it's taken years to build up mental pictures of these things.

Let's try a different approach. Say you're a tetrahedron manufacturer, a D&D dice maker, for example. You want to mark your tetrahedra, by colouring each vertex a different colour, say red, blue, green and yellow. How many ways can you do this?

Let's look at a top-down view of a tetrahedron and mark its positions.

We can assign any of the four colours to 1, so let's make it red, then vertex 2 can be any of the remaining colours, say we pick blue, then 3, make it yellow, and then 4 has to be green.

This is just one of 24 possible choices you could have made. But if you are shipping a bag of different coloured tetrahedra, would it be worth your while making 24 different types of tetrahedra with each of the different choices of colourings?

Well of course not, right? If one colouring can be achieved from another by picking up the tetrahedron, spinning it in and putting it back down again, then why bother colouring them separately to begin with? So I'd argue that you only need to make two coloured tetrahedra.

We can obtain twelve of the 24 configurations by rotations of one tetrahedron, and the other twelve configurations by rotating the other tetrahedron, but you can't go from any configuration of the first to any configuration of the second. Nature has drawn a line we can not pass.

Does this remind you of something? A little puzzle with fifteen sliding tiles in a 4X4 square, perhaps? https://www.cs.brandeis.edu/~storer/JimPuzzles/ZPAGES/zzzFifteen.html

So that was CASE 2: where we were thinking about colouring the tetrahedron from scratch rather than transforming a coloured tetrahedron in 3-d space.

There's still more you could do here to get to know the group of transformations better. See how compositions work, for example.

But I want to take a step back for a moment, and consider the tetrahedron and the square. What makes a tetrahedron more symmetric than a square, or at least have more symmetries?

The answer, in one word, is structure. In more words, it's about how the vertices interact.

The simplest, and my favourite, way to see this is to look at edges. Say I am teaching a computer, which has no geometric intuition. How do I explain to it what a tetrahedron is? How do I store a tetrahedron, or a square, ~as data~?

One way to do this is to describe geometric objects as lists of finite sets. We have been doing this already, in our discussion so far. Everything you need to know about a triangle you can know in terms of its vertices. To think about edges is to think about pairs of vertices.

Now if we are to think about squares and tetrahedra like this, both have four vertices, so what distinguishes them? Only we understand shapes in terms of dimensions, remember.
If you're an ant walking on the surface of a wire frame structure, how do you know what shape you're on?

In a square, every vertex has two neighbouring vertices and an opposite vertex. In a tetrahedron, the view from every vertex is the same, you see three identical vertices, reachable via an edge.

So we can strip all our sense of geometry away from these objects, and just think about them as lists. A list of vertices, a list of edges, a list of 2-d faces... Yes, we lose a lot of our understanding of objects this way, but we also, hopefully gain new ways of studying them.

So what is a square now? A set of vertices {A,B,C,D} and edges {AB, BC, CD, AD}, that describes a square for our purposes. Every transformation in the dihedral group of order eight swaps around (technical term: permutes!) the vertex set, in a way that “preserves” the edge set.

It’s worth stating this quite precisely before we go on. Say we have a set of n elements, where n is some natural number. A permutation is a mapping or function that sends the set to itself, so every element has a unique image, and no two elements map to the same image.

Say you are a meeting with n people and the organisers have provided everyone with a nametag. Everyone grabs a nametag without looking, and clips it on, so everyone has a name, but everyone is displaying a name that is a rearrangement of all your n names.

That map, where you are mapped to the person whose name tag you are wearing, that’s a permutation. Think of a little arrow going from you to that person. As we look at your group as a whole, everyone has exactly one arrow pointing away from them and one pointing at them.

Note that this can be the same arrow. This is not like the Secret Santa situation where your arrow can’t point at yourself.

Now you can compose permutations of a set over and over and you will always end up with permutations. ie, draw a new set of such arrows from each element to another (including itself), then you get a new image by starting at each element, follow the first arrow then the second.

There is also a zero-permutation, where everyone’s arrow points at themselves, and every permutation has a reverse permutation, where you just reverse the direction of the arrows.

So permutations of a given set also form a group!

Or I should rather say, a group is a mathematical structure that we defined as an abstract distillation of this nice, self-contained nature of transformations of geometric objects, sets, etc.

So the symmetries of the triangle? That’s the group of all permutations of a set of size three.
The number of colourings of a tetrahedron’s vertices? That’s the group of all permutations of a set of size four!

The symmetries of the square and the solid transformations of the tetrahedron? They act as permutations on the set of vertices of these objects, and form what we call subgroups of the full group of all possible permutations.

How many permutations are there of n things? Pick one thing, draw an arrow to any of the n things, pick another, you have n-1 arrows you can draw, n-2 for the next and so on until the last one goes to the last remaining image. So n.n-1.n-2...1 possible permutations.

We call the number of possible permutations of n objects “n factorial” and denote it “n!”.

1!=1
2!=2
3!=6
4!=24
5!=120
6!=720
7!=5040
8!=40320
9!=362880
10!=3628800
... and so on.

See how fast it grows?

We call the group of all permutations of n things “the symmetric group on n elements” and denote it Sym(n). So that’s a third infinite family of groups to play around with.

Note that it doesn’t matter what the elements are, just how many there are. The particular elements can be substituted for each other, as long as there is no structure in how they relate to one another.

For example, our tetrahedron has four vertices, which are indistinguishable in terms of their relationship to one another, any two form an edge, any three form a triangular face. Whereas a square has additional structure. Some pairs of vertices are edges, some are diagonals.

In Alexander Masters’ book about the mathematician Simon Norton, he describes the symmetric group as a garbage bag group. It’s an analogy that has stayed with me. If you put n things in a garbage bag, however you shake them about, you still have a garbage bag with those n things.

That’s not being mean to symmetric groups. They are beautiful and incredibly interesting, and thousands of people have spent countless hours trying to understand them better. But as far as how they act on sets of objects, they show too much symmetry and not enough structure.

I guess what I’m saying is, sometimes there is a tension between structure and symmetry, and for me, mathematical beauty is when you find the right balance of both.
I’m going to potter about in the kitchen now, if I don’t pick this up again this evening, I’ll be back tomorrow.

As always, https://twitter.com/yet_so_far/status/1270434956557377536?s=21 https://twitter.com/yet_so_far/status/1270434956557377536

Right, where were we? We met the symmetric groups, and saw that they describe all the permutations of a set of a given size, and as you add structure to your set, this reduces the possible symmetries and gives you subgroups of the symmetric group. e

For example, the square is more structured in this sense than the tetrahedron, and it has only eight out of 24 possible symmetries.

What about the twelve solid rotations of the tetrahedron, can they be captured in terms of a subgroup?

Well, sure, we described the transformations in CASE 1 for the tetrahedron, and you can check from a composition table that they do form a subgroup of Sym(4). What I’m really wondering is, can we describe this particular group purely combinatorially, ie in terms of vertices etc.?

That’s something I want to come back to, but let us go back to the geometric objects we were considering, the Platonic solids. What are the symmetric groups of the remaining four: the cube, the octahedron, the dodecahedron and the icosahedron?

Let’s look at the cube. It has eight vertices, twelve edges, and six square faces. What are its symmetries?

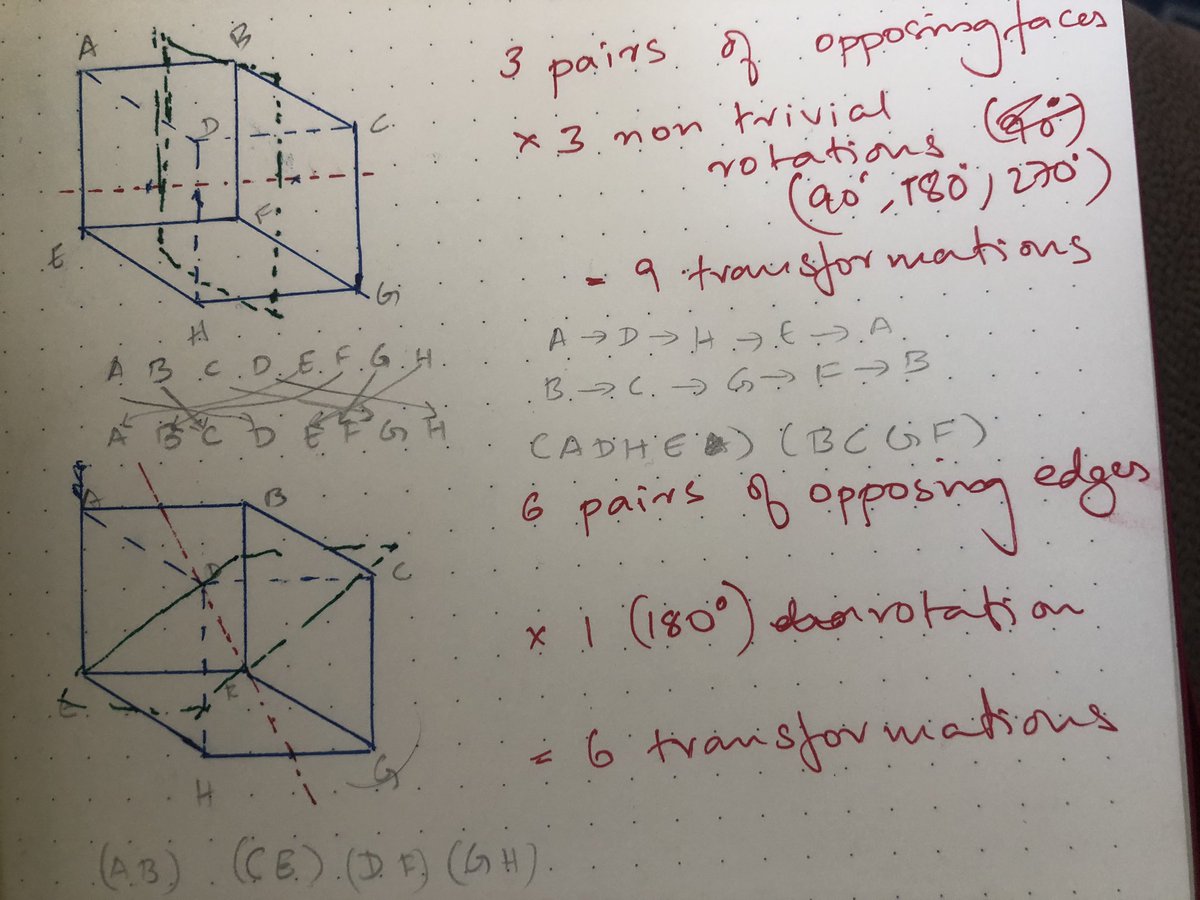
Shall we start by counting how many there could possibly be, if we didn’t insist on the transformation being achievable in 3-dimensional space?

Pick any vertex, call it A, a transformation could send it to any of the eight vertices, pick one. Now what of its three neighbours?

They have to go to the three neighbours of the image of A. We have six ways of picking those three vertices, so 48 transformations max, if we didn’t pay attention to the physics.

And how about if we did pay attention to the physics? Let’s try and imagine a rotating cube and ask, what axes and what rotations can we identify that preserve the structure of the cube?

Did you find 24? I don’t want to give you all the details, figuring stuff out for yourself is half the fun.

But drawing the right picture is also half the fun, which I reserve the right to have, so here’s a picture.

How do we satisfy ourselves that these form a group? We could name each vertex and write the permutation of the vertex corresponding to the transformation with arrows, that’s one way. If you try that, you’d see it gets quite messy to write down and even worse to type.

So some thrice blessed soul came up with a way of writing down permutations which is not only more efficient, but better to calculate with.

(They shouldn’t just give prizes and recognition for proving theorems and such, finding the right notation for things is equally valuable.)

So what is this miraculous notation?

The key observation that enables us here is that if you have a permutation, which is a set (of size n), together with n arrows such that each element has an arrow pointing away from it and one towards it, you can chase these arrows around.

Start at the first element, then look at where its arrow points, its image, call it I(1), now look the image of that, I(I(1)), and so on until the arrow eventually comes back to 1.

Why does this have to happen?
Because there is an arrow that comes back to 1 and only finitely many arrows.

Why won’t it come back to any other intermediate image?
Because there is only one arrow pointing at any element, and we have already identified it.

So every element belongs to a unique cycle of arrows, and you can write down a permutation as the collection of cycles of the form (1, I(1), I(I(1)), ... , 1) etc.

Distinct cycles in the same permutation are disjoint, ie no element of our set belongs to multiple cycles.

Here’s some of the permutations from our picture of the cube written out in cycle notation.

Note that even though the order in which we compose permutations does influence the outcome, within a permutation, if you look at these cycles as “sub-permutations”, they act on disjoint subsets, and can be applied in any order.

Mantra: “Disjoint cycles commute.”

Cycle notation also gives us a nice way of seeing the “orders of elements” in a permutation.

We said that the order of a group is the number of its elements. The order of a group element is the number of times you compose it with itself to get back to the zero-transformation.

For example, you can see that in the geometric objects we have considered so far, reflections have order two, and a rotation by a 360/n degree angle has order n.

In permutations, a cycle of length k (ie has k elements, we don’t usually close with the first element) has order k.

Orders of elements are handy to know, I use them mostly to distinguish groups from one another. But let’s crack on with trying to understand the symmetries of the cube. Are there any more than the symmetries we identified? Can we compose our 24 symmetries to get new ones?

Well, now that we have cycle notation, what about we try and use that to write down compositions of elements without quite drawing pictures?

Let’s try an example, compose the 90 deg rotation
(ADHE)(BCGF)
with the 180deg rotation
(AB)(CE)(DF)(GH).

We apply (ADHE)(BCGF) first, so A—>D, then in the second one D—>F, so A maps to F in the composed permutation. Now look at where F goes. F—>B—>A. So our first cycle is (AF).
Now chase B around. B—>C—>E and E—>A—>B, so we have (BE).
Similarly (CH) and (DF).

Now what if we reverse the order of the permutations we compose? Do you get
(AC)(BD)(EG)(FH)?

And if you step back and look at the geometry, how the transformations affect the axes of rotations, hopefully you’ll find nothing too surprising?

It’s useful to build up a fluency with thinking about one thing in many ways, and to translate between those ways. Think of symmetries of geometric objects as structure-preserving permutations of their vertex sets, but also build mental geometric models of combinatorial objects.

We will come back to this very idea shortly, it’s basically all I do in my so called “research career”, but I want to tie up and put a bow on our discussion of the cube and the Platonic solids.

So the cube, you can finish its table of compositions if you like, and write out all 24*24=576 table entries, and if you want to think geometrically, just look at the axes, and ask, what happens when I compose a rotation of this here type with one of that there type?

And what of the 24 remaining “physically impossible” transformations, remember we said there were 48 in total? https://twitter.com/yet_so_far/status/1271871178869800960?s=21 https://twitter.com/yet_so_far/status/1271871178869800960

You can imagine these as reflections about planes that divide the cube into mirroring halves. Moreover, each plane of reflection is perpendicular to an axis of rotation we identified earlier! So we have 3+6+4= 13 reflections, are there more?

Oh no wait, that’s not quite right, is it? Reflecting about planes perpendicular to these first two types of axes is fine. So we have nine we can be quite confident about.

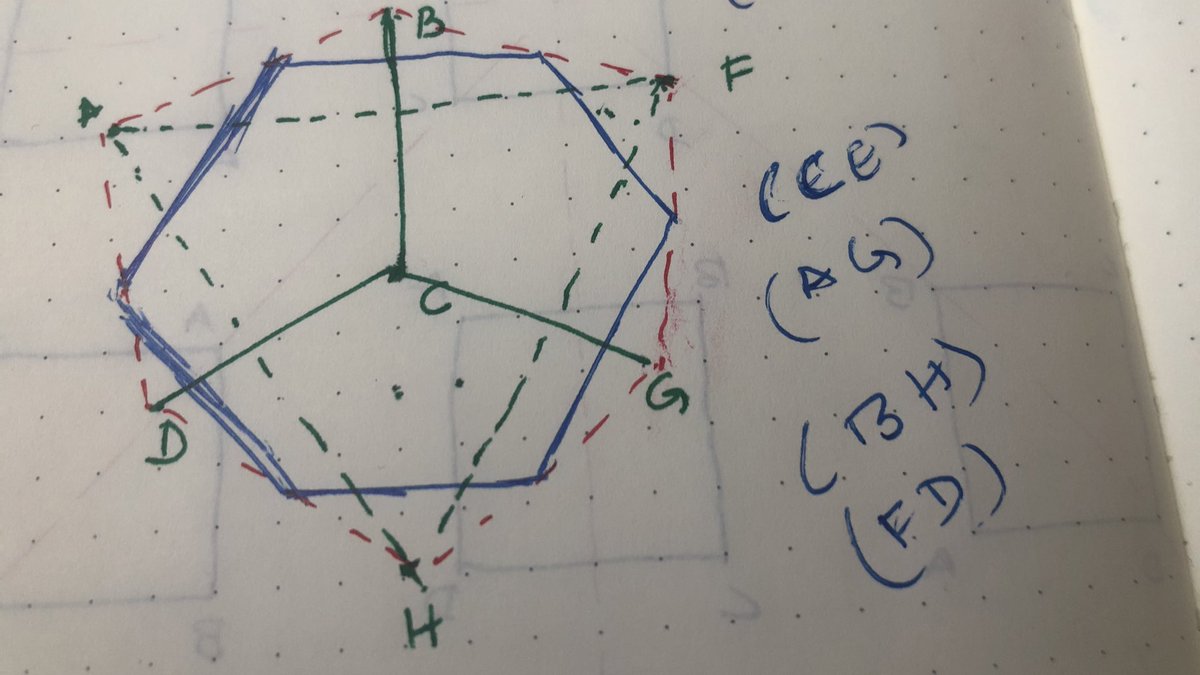
But let us think more carefully about the last four. Here the axes join a vertex to its opposite vertex. What is the “equatorial plane” perpendicular to any one of these axes?

Using your imagination, a physical model, or google, convince yourself that this is a hexagon.

There are six edges that do not contain the two vertices you picked. This vertices of this hexagon are the midpoints of those edges. Here is a picture, if it helps.

What does reflection about this plane look like? If I swap C and E in the picture above , the other vertices end up in positions that weren’t previously occupied by vertices, so that reflection is not quite a symmetry.

But, it’s still very close to being a symmetry!

You could reflect and rotate the cube just a little bit (60deg to be exact) to get a symmetry. In cycle notation, we could describe one of these as
(CE)(ABFGHD),
which also shows you that it’s different from all the symmetries we identified before. (Why?)

What if I compose this transformation with itself?
We get
(AFH)(BGD)
which was already one of our solid rotations. (You should also ask yourself why we can’t just keep the (CE) transposition and just rotate the hegagon as we like.)

What about applying the above transformation three times? We get
(AG)(BH)(FD)(CE)
which is a new type of transformation that swaps all pairs of opposing vertices that we can’t obtain through solid rotations.

So we have 4*2=8 rotations for each pair of opposing vertices, with a reflection combined with a 60deg turn either clockwise or anti-clockwise. And one uber-reflection that you get when you compose any of these transformations three times.

Oh and here’s a picture that helped me.

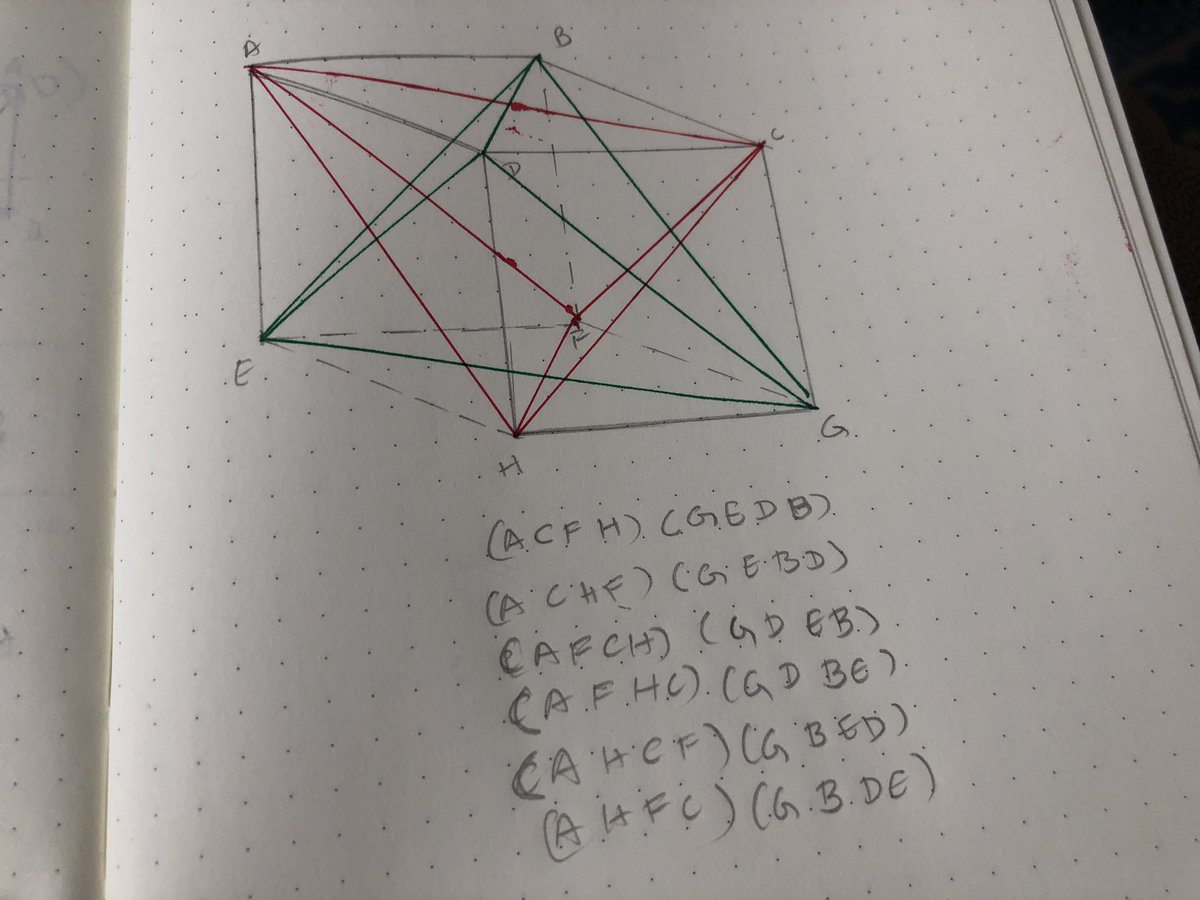
So we’ve identified 18 transformations not obtainable through rotations of a solid cube, and we know that there are at most six left. So we stare at the cube some more, and since we are trying to find six of something, go back to the first two pictures of types of axes.

Right, I really don’t want to lose this thread, so I’ll try and make some progress on this today. So we were talking about transformations that preserve the geometry of the cube, yet are not possible via rotations. And there are six remaining. I’ll tell you what they are.

First, recall that every vertex in the cube has three neighbouring vertices, three vertices “two edges away”, and an opposite vertex. Given any vertex, the three vertices two edges away are also two edges away (or at distance 2) from each other.

What happens if you draw diagonals across each face that connects each vertex to the vertices at distance two from it?

That’s right, you get two regular tetrahedra, whose edges are the face-diagonals of the cube! (This, to me is a miracle, something I never cease to wonder at. You are of course free to differ.)

And what do the six transformations do? They induce single-cycle permutations on the vertex sets of each tetrahedron that cycle the vertices about. And there are exactly six of them!

I found these quite hard to imagine, but quite easy to work out with group theory. If you have a good way of “seeing” these transformations, I’d love to know.
But I still think we are getting to a stage where the algebra starts to reveal its power, and leaves the geometry behind.

Or to be more precise, we are coming to a stage where it’s easier to chase symbols around a page (do algebra) than to imagine and describe shapes twisting and turning in higher dimensional space (do geometry). So this is a good time to spend some time on groups themselves.

We have talked about groups as collections of transformations of sets with structure. They are self contained in the sense that composing transformations in a group gives you transformations in the same group. And similarly self contained subsets of groups are called subgroups.

And subgroups are often the transformations that preserve certain kinds of structure, or respect certain kinds of restrictions. e.g., the subgroup of 3-d rotations among all possible transformations, or the subgroup of all transformation that preserve a cube inside Sym(8).

Notice how I said “a cube” just now? Why did I do that?

Just as we looked at a tetrahedron and said there are fundamentally two ways of colouring the vertices of a tetrahedron, we could ask how many fundamentally different ways there are of colouring the vertices of a cube.

There are 8!=40320 ways of assigning colours to the vertices of a cube. Also each colouring is equivalent to 24 colourings obtainable through solid rotations. So that gives 40320/24=1680 fundamentally different colourings.

Now I want to do some self-indulgent counting to convince myself that this is indeed the case. (Self indulgent because I already know this is true, because of something called the orbit-stabiliser theorem.) But I’m trying to figure stuff out in the most explicit way I can, so.

Start with a set of eight colours, Pick any vertex, call it A, and colour it. Then you have seven choices for the opposite vertex B. Now look at A’s three neighbouring vertices, call them C, D and E. They look identical from the point of view of A and B.

There are twenty ways of choosing three colours out of six. (Exercise!) And you can arrange your chosen colours in two distinct orientations. And now your three remaining colours are distinguished by their neighbors, so there are 6 ways of colouring them.

7*20*2*6=1680.

Now for another question. For every choice of colouring, you have a group of 24 solid rotations of the coloured cube. How are we to think about these 1680 groups? Are they different, or are they the same?

Even though they are distinct subgroups of Sym(8) you can obtain any of them from any of the others by simply renaming the vertices. We say all copies of the group of symmetries of the cube within Sym(8) are ISOMORPHIC to each other.

Also, even if we didn’t stick with the same set of colours or names, if we have a way of relabelling the vertices so that the symmetries preserve the same structure, we have an isomorphism of groups.

There is one more thing i want to say about isomorphisms before we move on.

Let’s go back and have a look at that view of the cube with two tetrahedra inscribed in it. We can think of these tetrahedra as opposing pairs.

In the sense that the action of any symmetry of the cube on one tetrahedron also determines what happens to the tetrahedron made of its opposite vertices, and has a sort of mirror action. In fact the symmetries of the cube act as permutations of the set {{A,G},{B,H},{C,E},{D,F}}.

... which has size four and at most 24 permutations. So how does that line up with the 24 rotations and 48 more general symmetries of the cube? I won’t bore you with the deets, but the 24 solid rotations of the cube act as the full set of permutations of the pair of tetrahedra.

When you come across a transformation that’s one of the 12 impossible ones for the tetrahedron, the cube gets around this by swapping the two tetrahedra themselves. (I see you nodding along, people who know about parities of permutations, but I won’t get into that right now.)

Anyway, to get to my point, the rotational symmetries of the cube are same as the full symmetries of the tetrahedron, Sym(4). The two groups, even if they act on sets of different sizes and structures, are still isomorphic. They have the same shape.

Enough of the cube. But for such a simple, familiar, object, it does open up a whole world of group theoretical concepts. I won’t say much about symmetries of the octahedron, as the octahedron is dual to the cube.
Every face of the cube corresponds to a vertex of the octahedron.

And what about the remaining dual pair of platonic solids, the dodecahedron and icosahedron?

They have 60 rotational symmetries: a vertex of the icosahedron can be mapped to any of 12 vertices, and once that is done, you have 5 rotations. There are 120 combined with reflections.

We’ll come back to this group and study it in more detail, it’s a great jumping off point for the thing I‘m working towards talking about, a special property of the number six. But I’ll stop for now, gather my thoughts, and most importantly, check back to see if I’m making sense.

Back tomorrow, but until then, let me know if you’re still here! I have been skipping over more and more detail, but I’ve left nothing out that you couldn’t get pen and paper out and work out for yourselves, hopefully.

So I read back over this, and am happy to report that I’m still making sense to myself, at least. But I’m just remembering stuff I know, and it may not be easy if you haven’t seen this before.
What I do hope is that anyone reading this gets a sense of the kind of thinking we do.

There is a lot to talk about, to gaze and wonder at, even in the simplest of objects and their symmetry groups. Not least of which is the significant amount of numerology around groups. Some numbers show up often, usually the products of the smallest primes. They make stuff work.

So back to groups, we saw that geometric shapes in two and three dimensions with some symmetry have groups associated with them. And in higher dimensions? One notable family of objects is the analogue of the triangle and tetrahedron, the simplex that exists in every dimension.

My favourite way of thinking about the n-dimensional simplex is as follows: Take n+1-dimensional space (she says, as if it’s no big deal) and look at its n+1 standard coordinate axes. Your x,y,z... Along each, pick the point at distance 1 from the origin. These are your vertices.

Add all possible edges, triangular 2-d faces, tetrahedra 3-d faces etc.

Or purely combinatorially, an n-dimensional simplex is a set of size n+1 together with all its subsets.
And hopefully that tells you that its group of structure preserving symmetries is Sym(n+1).

To me, the n-dimensional simplex is a good geometric model to think about the actions of the symmetric group Sym(n+1).
But mostly when I think about groups using geometric models, I like to think about graphs.

No, no, not that kind of graph, the ones with vertices and edges. A simple way of encoding information about a set of objects and the existence of some relationship among them. The vertices are the objects, and we jointwo vertices by an edge if they satisfy said relationship.

Sometimes the structures we study get quite complicated, has many types of subobjects with internal relationships, and we associate multiple graphs to it. Sometimes we see things better when we colour parts of the graph. I find them the simplest to doodle and see stuff.

If I am thinking about the n-dimensional simplex, I find it useful to draw the complete graph on n+1 vertices, K(n+1). Anything I want to think about the symmetries of the simplex, I can translate to a symmetry of the graph, and it's quite useful and easy to think this way.

And graphs themselves have symmetry groups, called automorphism groups. (In general, the symmetries of combinatorial structures are called automorphisms. An automorphism, as the name suggests, is an isomorphism from a structure to itself.)

But what is a graph automorphism?

We define it as any function permuting the vertices of the graph so that if two vertices in the graph are related (joined by an edge), then their images are also related.

Think of it as a redrawing of a graph, a way of rearranging the vertices without breaking or adding edges.

Remember how we talked about the automorphisms of regular polygons in the plane? We were basically talking about them as graphs, cyclic graphs to be exact, and their automorphisms are the dihedral symmetries we constructed.

Let's look at an even more interesting example.

To do that I want to introduce the projective plane.

I know, I know, this thread is already A Lot, but I'm having fun so I'm not going to stop.

So.

How do I describe projective space? Let me count the ways.

There are a few ways of understanding the real projective plane.

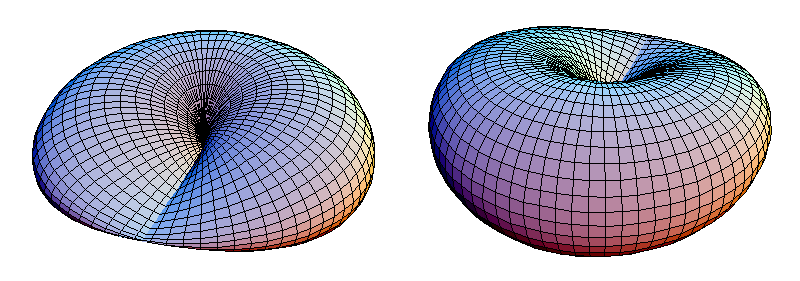
The real projective plane is the antipodal quotient of the 2-dimensional sphere. And what do we mean by that?

Your 2-d sphere is the surface of the ball in three dimensions. Every point on the sphere has a point directly opposite it (if you look from a point through the centre).

So what we do is imagine a space where every point is identified with its opposite or antipodal point.

It's a hard one to picture. Will it help if I say the real projective plane (RPP) can be thought of as the set of all lines through the origin (0,0,0) in 3-d space?

Why did anyone come up with such a weird space? Well, it describes a world where "parallel lines meet at infinity", which many people find easy to believe in. It has a long and fascinating history which I won't go into here.

Here's one more way of trying to picture the RPP: Take the 2-d sphere and cut it into three, a northern hemisphere, a southern hemisphere and an equator separating them. Now imagine one of the hemispheres rotating by 180 degrees and lining up with the other.

That's the antipodal identification on the two hemispheres. Then equator twists into a figure eight space, and folds in on itself. Finally, glue the points of the equator back on to the boundary of the hemispheres.
This is the cross-cap model of the RPP. Here's a sort of picture.

It's impossible to draw the RPP in 2d or 3d without bits crossing over each other. But in 5 dim.s and up, the RPP lives with no crossings. It's like how some graphs have crossing edges however you draw them on a plane, but all graphs can be drawn with no crossings in 3d space.

Right, why do we care about this really weird geometric object? Weren't we talking about rather discrete structures, sets and their subsets and groups acting as permutations and all that?

Well, I want to make a discrete model of the real projective plane.

What to I mean by that? How do we make discrete models of such things, with their smooth curves and infinitely many points?

One way is to break up space into linear, flat, whatever the higher dimensional analogue of that is, pieces, each of which we can describe combinatorially.

For example, you could say that every polygon is a way of approximating a circle with linear pieces or line segments. Every polyhedron, the platonic solids, for example, is a way of approximating the sphere with flat polygonal discs, bounded by triangles, squares, pentagons etc.

We can do this in every dimension, breaking up 3-d space into tetrahedra, cubes etc., higher dimensional space into higher dimensional simlipces and hypercubes so on.

I want to look at a very specific case, where the given space is always broken up into simplices.

So in 1-d an object like a circle is still modelled by polygons. In 2-d, the sphere, is modelled by things like the tetrahedron, octahedron, icosahedron, and other less nice polyhedra, as long as the faces are triangles, we are good, 3-d spaces are made of tetrahedra, and so on.

A collection of simplices, which also meet in their lower-dimensional subsimplices is called a simplicial complex. In combinatorial language, it is a collection of sets such that every time a set is in that collection, all its subsets are also in the collection.

A "simplicial complex model" of a geometric space is called a triangulation. There's a key caveat here, we should be able to describe every simplex in terms of its vertex set. e.g, if I say "the edge AB", there should be no ambiguity, so there should be a unique edge between A&B.

So polygons, (with at least three edges), triangulate the circle. Polyhedra with triangular faces triangulate the 2d sphere, the set of all proper subsimplices of the k+1 dimensional simplex triangulate the k-dimensional sphere.
Can we triangulate the Real Projective Plane? How?

Answers tomorrow!

And the answer is... yes! You can trianglulate projective space of any dimension, and this whole detour into projective space was to show you one particular triangulation of the real projective plane. This one:

So what are we looking at here? At first glance we seem to be looking at a face of the icosahedron, all three faces that share an edge with it, and all six more faces that share an edge with those! Ten faces, that’s half an icosahedron.

Now have a closer look at the boundary.

You see a hexagon, but its vertices are 123123. When you see that kind of repetition in mathematical pictures, it means we are talking about identification. Think of vertices and edges with the same label as glued together. The boundary hexagon twists, folds into a triangle.

Isn’t this the same as the cross-cap disc model we were talking about earlier? I’ll leave you to check that it is. And if you have an icosahedron handy, do check that this is also its surface with opposite points identified, what we call “the quotient mod the antipodal relation”.

Another this you can check is that this triangulation has the fewest possible vertices (edges and faces too!) of any triangulation of the RPP. Why? Why can’t we quotient (ie, identify antipodal points of) an octahedron like we did an icosahedron?

What are its triangles? There are 10, namely
[124], [125], [135], [136], [146], [234], [236], [256], [345], [456].

A set of sets you can stare at for quite some time and notice quite a few remarkable properties of. It seems to have a lot of... symmetry!

Every vertex is in five triangles, and every edge is in exactly two triangles. Not very surprising when you consider that it’s basically half an icosahedron.

But also, every possible edge is in there, and exactly half of all possible triangles.

That’s not quite so easy to predict if you start with the icosahedron. And if you were just given the triangles, could you reconstruct an icosahedron? I don’t think that one’s very easy.

But we were drawing graphs, let’s get back to that.

What graphs could we draw here? There a quite a few choices. What if we draw one whose vertices and edges are the six vertices and fifteen edges of the complex? That would be the complete graph on six vertices, and wouldn’t quite capture the structure of the object we have here.

What if we, draw a graph whose vertices are the ten triangles of the complex? Then we have some choices for the edge set. You can join two graph-vertices (complex-triangles) by a graph-edge if
(a) they share an edge of the comple
(b) they share exactly one vertex of the complex

(c) both the above.

Since any 2 triangles meet either in an edge or a vertex, (c) gives you the complete graph K(10), again we’ve too much symmetry, not enough structure.

Also, the graphs described by (a) and (b) are complementary. The edges of one are the non-edges of t’other.

So let’s draw the one with fewer edges, it also feels more correct to draw, as meeting at an edge is more neighbourly than meeting at just a vertex.

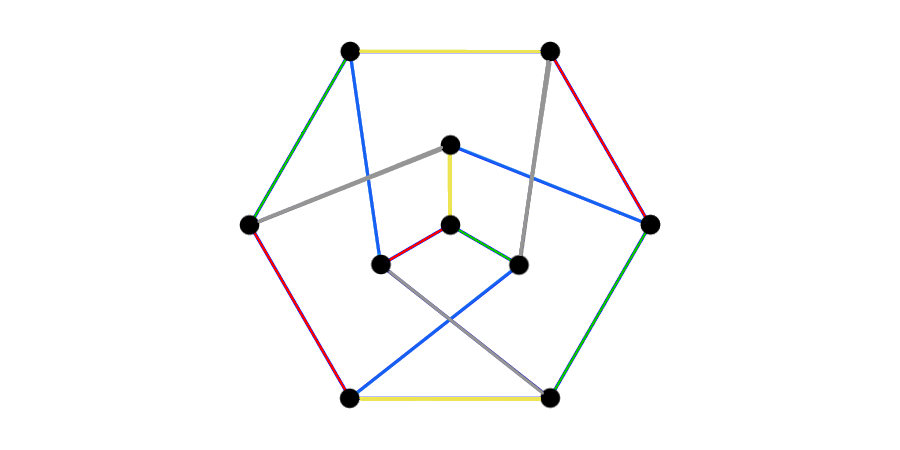
Here’s one I scrawled over the nice Wikipedia picture. What’s that graph?

What if I draw it a bit cleaner? You should check that this is the same graph as the one above, btw.

It’s a well known graph, important enough to deserve its own name. And it’s called the Petersen Graph.

What is the group of automorphisms of the Petersen Graph? You could buy the answer, if you like, on a T-shirt, and yes, I do have one. But let's try and work it out ourselves.

First observation, to start very naively, is that since an automorphism is a permutation of the vertex set, which induces a permutation of the edge set, there can be at most (size of vertex set)!=10!=3628800 permutations.

But we know we can do better than that.

We can argue, like before, that any vertex has 10 possible images under an automorphism, and then its three neighbours are mapped to the three neighbours of that, giving 3! ways, then the 2 remaining neighbours of any of those can be chosen in 2! ways, which fixes the rest.

(That last part is worth verifying on your own, by the way.)

But it is correct, and this argument gives 120 automorphisms. But there are many groups with 120 elements, so can we narrow it any further?

Well, let's take another look at the Petersen graph, and remember that automorphisms permute not just vertices, but also edges of a graph. In addition, they preserve the structural elements of any object. e.g, the image of a pentagon (5-cycle) will still be a pentagon.

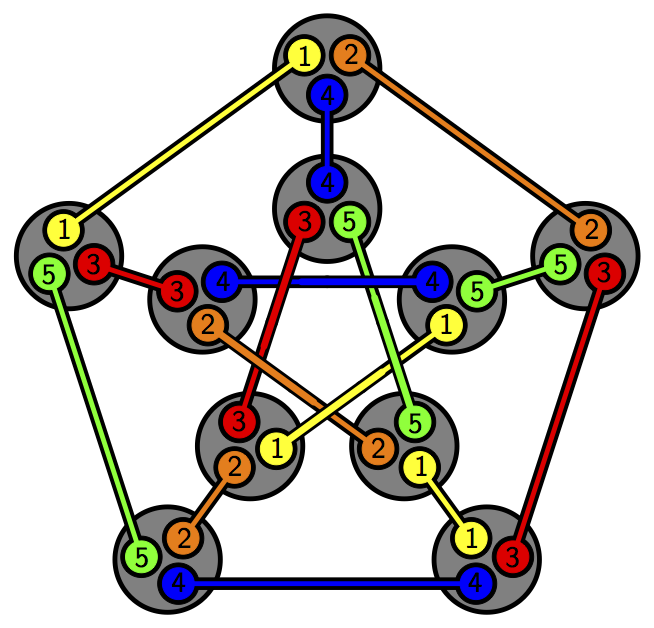
Well, to highlight a particularly useful structural element of the Petersen graph, I have coloured its edges. And what do we see now? Do you see how the 15 edges of the graph split into five sets of three edges, where the edges in each set are maximally distant from each other?

So how does that help us identify the automorphism group? Well, say an automorphism maps one of the yellow edges, say to a green edge. Then to preserve the distances between the edges, all the yellow edges must map to green edges. Automorphisms permute the colours of these edges.

Okay that was a bit too cryptic, maybe. What I mean is whatever automorphism preserves the structure of the Petersen graph, (I'm going to call it P from now, and I'll call the group Aut(P)) It acts on the set of colours we have above by permuting them.

Also, in P, just as in most objects we considered, the edges are in a sense identical to each other. In what sense? In that there is always a symmetry that maps any edge to any other edge. We say, in such cases, that the group acts TRANSITIVELY on the edges.

You can change edges to vertices in the previous, and get statements like "the group acts transitively on the vertices of this graph." In P, both are true. Aut(P) acts transitively on the vertices as well as the edges. It also acts transitively on the partition of edges above.

That was a something I probably should have mentioned earlier. Anyways, not only does Aut(P) act transitively on the set of colours (which is just visual shorthand for the partition into sets of three mutually maximally distant edges), it acts as the full symmetric group on it.

In the case of our P with the coloured edges, we can swap e.g, for example, by swapping the following vertices.

Okay, we’re omitting a few details here, but they can be worked out, and are sort of tedious to work out On Here. I just wanted to sketch the broad argument and point out some interesting features of the symmetries of P. Anyway, if you buy my last assertion, the takeaway is...

Aut(P) contains a copy of Sym(5).
And since Aut(P) has size 120, and so does Sym(5), Aut(P) is isomorphic to Sym(5), like the T-shirt said.

So what we saw here is different Sym(5) actions, transitive actions, on sets of size 5 (colours), 10 (vertices of P), and 15 (edges of P).

I think that’s very cool. But there’s one more Sym(5) action which I think is the nicest of them all. And that’s its transitive action on six points.

I’ll give you till tomorrow to figure out which six points, imaginary and very unlikely person who read this far.

But before I do that, here's another picture you can manipulate in your head to convince yourself that every element of Sym(5) acting on the colours induces an automorphism of P. This is by @japhethwood, via the excellent Visual Insight blog. https://blogs.ams.org/visualinsight/2015/07/01/petersen-graph/

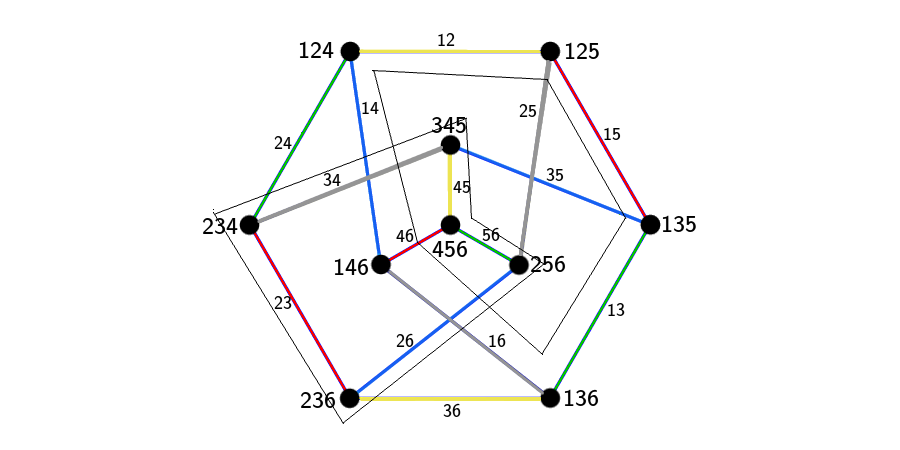
Now, for the Sym(5) action on six points. Where did we see a set of six points recently? That's right, the six vertices in the triangulation of the RPP which started this whole thing off. Every vertex of P is a triangle in that complex, so let us bring those labels back.

And what happens to the six numbers 1... 6 when we apply automorphisms of P to its vertices and edges? I want to add a bit more labelling to the picture above, and this time I label the edges of P, in what is hopefully the most obvious way.

Every edge is labelled by an edge of the triangulation of the RPP. See how all fifteen possible edges are in there? And see how, for every one of the five edge-colours, the set of three edges of that colour partition the vertex set {1,...,6} into edges? Do keep that in mind.

Anyway, the numbers {1,...,6}. To see what Aut(P) does to them, let us try and trace these numbers on the edge set of P. Look at 1, say, and look at the edges where 1 appears in the label. (Sorry I missed two labels in the previous picture). But look what we have. A pentagon!

And every pentagon comes with an opposite pentagon traced by its not vertices. There are six such pairs. And what do automorphisms of P do to these pentagons?

Let us pick one and find out. Say we pick the automorphism we talked about earlier, the one that swaps red with green.

It maps the Yellow-Red-Green-Grey-Blue pentagon to the Yellow-Green-Red-Grey-Blue pentagon.
(Oh yes, those cyclically ordered colours describe each pentagon uniquely. There are 12 *10 pentagons if you count all rotations and reflections, and 5! ways of ordering the colours).

But since we want to know how that translates to an action on the set {1,...,6}, let's look at what happens to the edge labels.
Red<-->Green maps
12--15--13--16--14 to 36--13--15--35--26
and
23--34--45--56--26 to 24--34--45--46--14.

If we index each pentagon pair with a number, and one does suggest itself quite readily, (since for any given element of {1,...,6}, each pentagon pair has one pentagon where every edge label contains that element,) the transposition Red<-->Green "maps 1 to 4".

Okay, what else do we have? What happens to pentagons 2,3,4,5 and 6? We can look at what this does to the colour orders and see that
1<-->4, as <-->
2<-->5, as <-->
3<-->6, as <--> .