Spent some time investigating history of "double descent". As a function of model complexity, I haven't seen it described before 2017. As a function of sample size, it can be traced to 1995; earlier research seems less relevant. Also: I think we need a better term. Thread. (1/n)
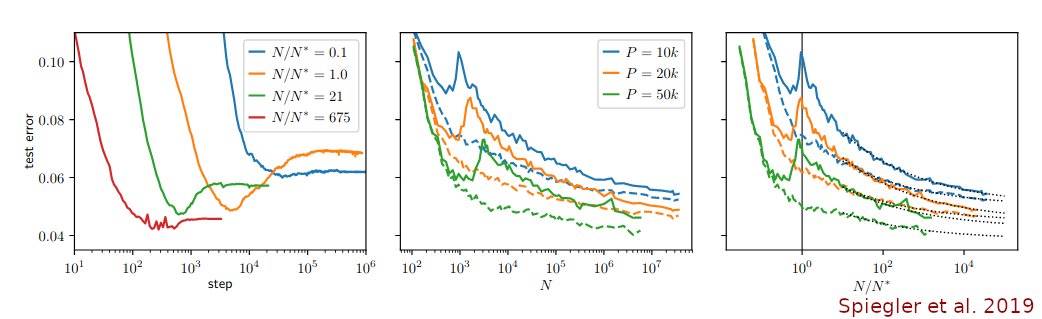
The term "double descent" was coined by Belkin et al 2019 https://www.pnas.org/content/116/32/15849 but the same phenomenon was also described in two earlier preprints: Spigler et al 2019 https://iopscience.iop.org/article/10.1088/1751-8121/ab4c8b/meta and Advani & Saxe 2017 https://arxiv.org/abs/1710.03667 (still unpublished?) (2/n)
I don't like the term "double descent" because it has nothing to do with gradient descent. And nothing is really descending. It's all about bias-variance tradeoffs, so maybe instead of the U-shaped tradeoff one should talk about \\/\\-shaped? И-shaped? UL-shaped? ʯ-shaped? (3/n)
@PreetumNakkiran et al. drew attention to the fact that the same \\/\\-shape happens also as a function of sample size: see ICLR 2020 https://openreview.net/forum?id=B1g5sA4twr and his follow-up preprints. The reviews on Openreview are interesting because they point to some much earlier work. (4/n)
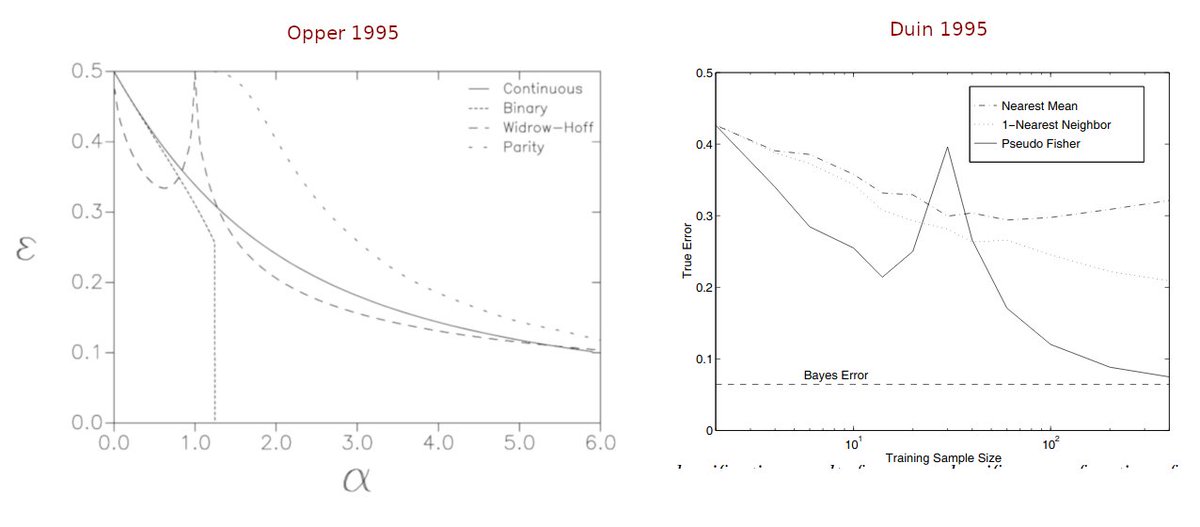
Specifically, Opper 1995 (in The Handbook of Brain Theory and Neural Networks) reported \\/\\-shaped risk (as a function of sample size) for a linear model http://www.ki.tu-berlin.de/fileadmin/fg135/publikationen/opper/Op03b.pdf. See also Opper & Kinzel 1996 or Fig 10 in Opper 2001 review http://www.ki.tu-berlin.de/fileadmin/fg135/publikationen/opper/Op01.pdf (5/n)
Furthermore, from this tweet I learned about the work of Duin and found Duin 1995 independently from Opper 1995 reporting the same thing: http://www.rduin.nl/papers/scia_95.sssize.pdf. See also Raudys & Duin 1998, Loog & Duin 2012, etc. (6/n) https://twitter.com/jan_gemert/status/1212465516444561416
Duin calls this "peaking phenomenon" and says it goes back to 1960s, but I don't quite get it. E.g. here Duin cites Hughes 1968 https://ieeexplore.ieee.org/abstract/document/1054102 but I think there it's just standard U-shaped underfitting/overfitting tradeoff, isn't it? (7/n)
Duin also refers (e.g. here http://37steps.com/2448/trunks-example/) to Trunk 1979 https://ieeexplore.ieee.org/document/4766926 as a "very clear" example of "peaking phenomenon", but there I also only see U-shaped overifitting. If so, I think the "peaking phenomenon" terminology is only confusing. (8/n)
I'd be very grateful for any additions/corrections to this historical overview. See e.g. this last work by @PreetumNakkiran for many more recent references. END. (9/9) https://twitter.com/PreetumNakkiran/status/1235376866715820032
PS. I should have pinged more authors of the mentioned papers: @advani_madhu @SaxeLab @mario1geiger @ilyasut @ShamKakade6 @tengyuma (and others).
PPS. Oh wow. See this answer and replies below. Thanks everybody for the ongoing discussion. https://twitter.com/SaxeLab/status/1243556473382342659
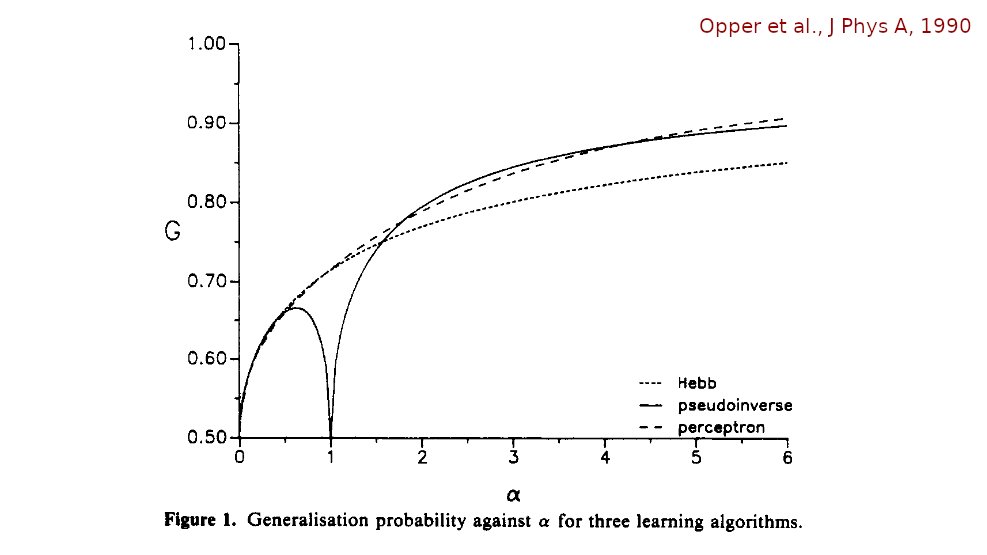
PPPS. @andrewgwils linked below ( https://twitter.com/andrewgwils/status/1243988946931060737) to his new preprint ( https://arxiv.org/abs/2003.02139 ) citing even earlier work by Opper for "non-monotonic generalization capability"! Here is Opper et al. 1990 https://iopscience.iop.org/article/10.1088/0305-4470/23/11/012:
PPPPS. @Tweetteresearch linked to his 1993 paper that led me to a bunch of 1989 papers from Opper, Kinzel, Krogh, and others, discussing divergence of the unregularized risk at P/N=1. But Opper 1990 still remains the reference with the earliest \\/\\ plot. https://twitter.com/Tweetteresearch/status/1244164920675049477

 Read on Twitter
Read on Twitter